题目内容
已知椭圆
的离心率为，且其焦点F（c，0）(c＞0)到相应准线l的距离为3，过焦点F的直线与椭圆交于A、B两点。
(1)求椭圆的标准方程；
(2)设M为右顶点，则直线AM、BM与准线l分别交于P、Q两点，（P、Q两点不重合），求证：
（1）
（2）见解析
解析:
（1）由题意有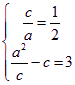
解得
∴椭圆的标准方程为 ……………………………………5分
（2）①若直线AB与
轴垂直，则直线AB的方程是
∵该椭圆的准线方程为
,
∴
，
， ∴
，
∴
∴当直线AB与轴垂直时，命题成立。
②若直线AB与轴不垂直，则设直线AB的斜率为
，
∴直线AB的方程为
又设
联立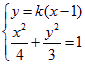
消y得 
∴
∴
又∵A、M、P三点共线，∴
同理
∴
，
∴
综上所述：
练习册系列答案
相关题目
已知椭圆的离心率为e，两焦点分别为F1、F2，抛物线C以F1为顶点、F2为焦点，点P为抛物线和椭圆的一个交点，若e|PF2|=|PF1|，则e的值为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
已知椭圆的离心率为
，焦点是（-3，0），（3，0），则椭圆方程为（ ）
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在由圆O：x2+y2=1和椭圆C：
如图，A，B是椭圆C：