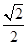题目内容
已知椭圆的离心率为e,两焦点分别为F1、F2,抛物线C以F1为顶点、F2为焦点,点P为抛物线和椭圆的一个交点,若e|PF2|=|PF1|,则e的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、以上均不对 |
分析:作PT垂直椭圆准线l于T,由椭圆第二定义知|PF1|:|PT|=e,又|PF1|:|PF2|=e,故|PT|=|PF2|,由抛物线定义知l为抛物线准线,故(-c)-(-
)=c-(-c),由此能求出e的值.
| a2 |
| c |
解答:解:作PT垂直椭圆准线l于T
则由椭圆第二定义
|PF1|:|PT|=e
又|PF1|:|PF2|=e
故|PT|=|PF2|
由抛物线定义知l为抛物线准线
故F1到l的距离等于F1到F2的距离,
即(-c)-(-
)=c-(-c)
得e=
=
.
故选C.
则由椭圆第二定义
|PF1|:|PT|=e
又|PF1|:|PF2|=e
故|PT|=|PF2|
由抛物线定义知l为抛物线准线
故F1到l的距离等于F1到F2的距离,
即(-c)-(-
| a2 |
| c |
得e=
| c |
| a |
| ||
| 3 |
故选C.
点评:本题考查椭圆的性质和应用,解题时要注意公式的灵活运用.

练习册系列答案
相关题目
 如图,A,B是椭圆C:
如图,A,B是椭圆C:
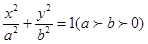 的离心率为e=
的离心率为e=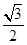 ,且过点(
,且过点(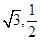 )
)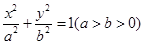 的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若
的离心率为e,焦点为F1、F2,抛物线C以F1为顶点,F2为焦点.设P为两条曲线的一个交点,若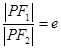 ,则e的值为( )
,则e的值为( )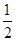 B.
B. 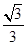 C.
C.
 D.
D.