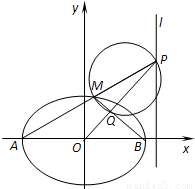
题目内容
 如图,A,B是椭圆C:
如图,A,B是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)若e=
| 1 |
| 2 |
(2)设直线AM交l于点P,以MP为直径的圆交MB于Q,若直线PQ恰过原点,求e.
分析:(1)由e=
,右准线l的方程为x=4,建立方程组,求得几何量,从而可求椭圆的方程;
(2)根据题意,可得A,M,P三点共线,MQ⊥PQ,由此可得几何量之间的关系,从而可求离心率.
| 1 |
| 2 |
(2)根据题意,可得A,M,P三点共线,MQ⊥PQ,由此可得几何量之间的关系,从而可求离心率.
解答:解:(1)由题意:
,解得
.∴椭圆C的方程为
+
=1. …(6分)
(2)设M(x,y),P(
,β),
∵A,M,P三点共线,∴
=
,∴β=
,…(9分)
∴-1=kOPkBM=
•
=
=
=
,
∴c2+ac-a2=0
∴e2+e-1=0,解得e=
.…(16分)
|
|
| x2 |
| 4 |
| y2 |
| 3 |
(2)设M(x,y),P(
| a2 |
| c |
∵A,M,P三点共线,∴
| y |
| x+a |
| β | ||
|
y(
| ||
| x+a |
∴-1=kOPkBM=
cy(
| ||
| a2(x+a) |
| y |
| x-a |
| y2(a+c) |
| a(x2-a2) |
| b2(a+c) |
| -a3 |
| (a2-c2)(a+c) |
| -a3 |
∴c2+ac-a2=0
∴e2+e-1=0,解得e=
| ||
| 2 |
点评:本题考查椭圆的几何性质与标准方程,考查学生分析解决问题的能力,考查学生的计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,A,B是椭圆
如图,A,B是椭圆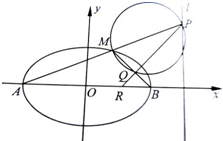 如图,A,B是椭圆
如图,A,B是椭圆 如图,A,B是椭圆C:
如图,A,B是椭圆C: 的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m.
的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m. ,m=4,求椭圆C的方程;
,m=4,求椭圆C的方程;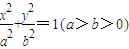 的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m.
的左、右顶点,M是椭圆上异于A,B的任意一点,已知椭圆的离心率为e,右准线l的方程为x=m. ,m=4,求椭圆C的方程;
,m=4,求椭圆C的方程;