题目内容
(1)已知椭圆的离心率为
,准线方程为x=±8,求这个椭圆的标准方程;
(2)假设你家订了一份报纸,送报人可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00-8:00之间,请你求出父亲在离开家前能得到报纸(称为事件A)的概率.
| ||
| 2 |
(2)假设你家订了一份报纸,送报人可能在早上6:30-7:30之间把报纸送到你家,你父亲离开家去工作的时间在早上7:00-8:00之间,请你求出父亲在离开家前能得到报纸(称为事件A)的概率.
分析:(1)设出椭圆的标准方程,利用椭圆的离心率为
,准线方程为x=±8,建立方程组,可求几何量,即可得到椭圆的标准方程;
(2)建立平面直角坐标系,确定父亲在离开家前能得到报纸的事件构成区域,以面积为测度,可得结论.
| ||
| 2 |
(2)建立平面直角坐标系,确定父亲在离开家前能得到报纸的事件构成区域,以面积为测度,可得结论.
解答:解:(1)设椭圆的标准方程为
+
=1(a>b>0)
∵椭圆的离心率为
,准线方程为x=±8
∴
∴a=4
,c=4,∴b2=a2-c2=16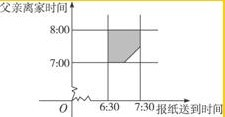
∴椭圆的标准方程为
+
=1;
(2)以横坐标表示报纸送到时间,以纵坐标表示父亲离家时间,建立平面直角坐标系,父亲在离开家前能得到报纸的事件构成区域是下图:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部分,就表示父亲在离开家前能得到报纸,即事件A发生,
所以P(A)=
=
.
| x2 |
| a2 |
| y2 |
| b2 |
∵椭圆的离心率为
| ||
| 2 |
∴
|
∴a=4
| 2 |

∴椭圆的标准方程为
| x2 |
| 32 |
| y2 |
| 16 |
(2)以横坐标表示报纸送到时间,以纵坐标表示父亲离家时间,建立平面直角坐标系,父亲在离开家前能得到报纸的事件构成区域是下图:
由于随机试验落在方形区域内任何一点是等可能的,所以符合几何概型的条件.
根据题意,只要点落到阴影部分,就表示父亲在离开家前能得到报纸,即事件A发生,
所以P(A)=
1-
| ||||||
| 1 |
| 7 |
| 8 |
点评:本题考查椭圆的标准方程,考查几何概型,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 的下焦点为
的下焦点为 、上焦点为
、上焦点为 ,其离心
率
,其离心
率 。过焦点F2且与
。过焦点F2且与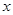 轴不垂直的直线l交椭圆于A、B两点。
轴不垂直的直线l交椭圆于A、B两点。 的值;
的值;  +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).