题目内容
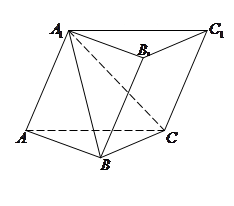
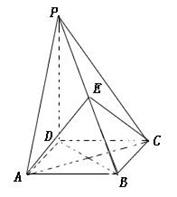
(本题满分14分 )如图,在三棱柱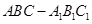 中,所有的棱长都为2,
中,所有的棱长都为2,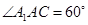 .
.
(1)求证: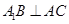 ;
;
(2)当三棱柱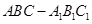 的体积最大时,
的体积最大时,
求平面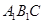 与平面
与平面 所成的锐角的余弦值.
所成的锐角的余弦值.
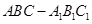 中,所有的棱长都为2,
中,所有的棱长都为2,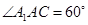 .
.
(1)求证:
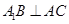 ;
;(2)当三棱柱
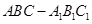 的体积最大时,
的体积最大时,求平面
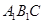 与平面
与平面 所成的锐角的余弦值.
所成的锐角的余弦值.(1)见解析;(2)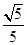 .
.
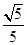 .
.(1)因为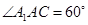 ,取AC的中点M,连接BM,A1M,可知三角形A1AC和三角形ABC都为正三角形,所以易证AC垂直平面A1MB,从而证得
,取AC的中点M,连接BM,A1M,可知三角形A1AC和三角形ABC都为正三角形,所以易证AC垂直平面A1MB,从而证得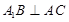 .
.
(2) 当三棱柱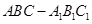 的体积最大时,点
的体积最大时,点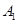 到平面
到平面 的距离最大,此时
的距离最大,此时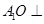 平面
平面 .由(1)知A1在底面的射影一定在直线BM上,并且三角形A1MB是等腰三角形,
.由(1)知A1在底面的射影一定在直线BM上,并且三角形A1MB是等腰三角形,
所以当O与M重合时,点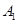 到平面
到平面 的距离最大.然后在此基础上再求二面角的大小即可.
的距离最大.然后在此基础上再求二面角的大小即可.

另解:当三棱柱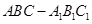 的体积最大时,点
的体积最大时,点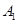 到平面
到平面 的距离最大,此时
的距离最大,此时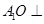 平面
平面 .以
.以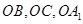 所在的直线分别为
所在的直线分别为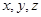 轴,建立直角坐标系,依题意得
轴,建立直角坐标系,依题意得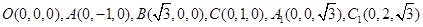 .
.
由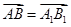 得
得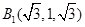 ,设平面
,设平面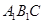 的一个法向量为
的一个法向量为
而 ,则
,则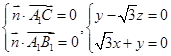 ,取
,取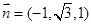
而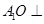 平面
平面 ,则平面
,则平面 的一个法向量为
的一个法向量为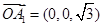
于是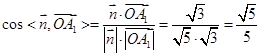 ,
,
故平面 与平面
与平面 所成锐角的余弦值为
所成锐角的余弦值为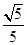 .
.
 ,取AC的中点M,连接BM,A1M,可知三角形A1AC和三角形ABC都为正三角形,所以易证AC垂直平面A1MB,从而证得
,取AC的中点M,连接BM,A1M,可知三角形A1AC和三角形ABC都为正三角形,所以易证AC垂直平面A1MB,从而证得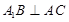 .
.(2) 当三棱柱
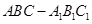 的体积最大时,点
的体积最大时,点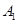 到平面
到平面 的距离最大,此时
的距离最大,此时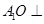 平面
平面 .由(1)知A1在底面的射影一定在直线BM上,并且三角形A1MB是等腰三角形,
.由(1)知A1在底面的射影一定在直线BM上,并且三角形A1MB是等腰三角形,所以当O与M重合时,点
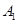 到平面
到平面 的距离最大.然后在此基础上再求二面角的大小即可.
的距离最大.然后在此基础上再求二面角的大小即可.
另解:当三棱柱
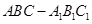 的体积最大时,点
的体积最大时,点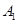 到平面
到平面 的距离最大,此时
的距离最大,此时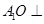 平面
平面 .以
.以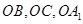 所在的直线分别为
所在的直线分别为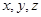 轴,建立直角坐标系,依题意得
轴,建立直角坐标系,依题意得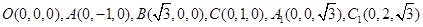 .
.由
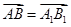 得
得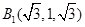 ,设平面
,设平面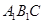 的一个法向量为
的一个法向量为
而
 ,则
,则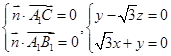 ,取
,取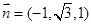
而
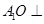 平面
平面 ,则平面
,则平面 的一个法向量为
的一个法向量为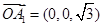
于是
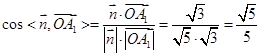 ,
,故平面
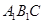 与平面
与平面 所成锐角的余弦值为
所成锐角的余弦值为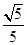 .
.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,底面
中,底面 是矩形,
是矩形, 平面
平面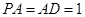 ,
,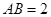 ,
,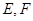 分别是
分别是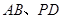 的中点.
的中点.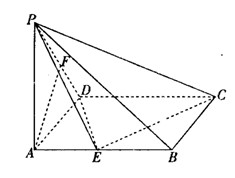
 平面
平面 ;
; 的余弦值.
的余弦值. 的底面是正方形,
的底面是正方形,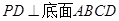 ,点E在棱PB上.若AB=
,点E在棱PB上.若AB=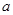 ,
,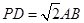
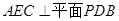 ;
; 
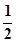 AD=1,CD=
AD=1,CD=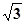 .
.
 ,
,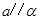 ,
,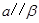 ,则
,则 与
与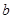 的位置关系是_______.
的位置关系是_______.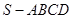 的底面边长为
的底面边长为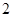 ,高为
,高为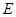 是边
是边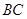 的中点,动点
的中点,动点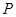 在这个棱锥表面上运动,并且总保持
在这个棱锥表面上运动,并且总保持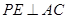 ,则动点
,则动点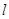 、
、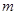 与平面
与平面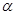 、
、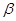 的命题中,正确的是 ( )
的命题中,正确的是 ( )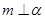 ,
,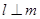 ,则
,则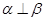 ,
,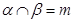 ,
,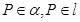 ,且
,且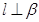
 ,
,
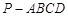 中,
中,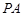
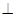 平面
平面 ,底面
,底面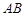 ⊥
⊥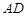 ,
,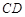 ⊥
⊥ ,
,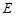 为
为 中点.
中点.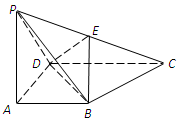
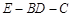 的余弦值.
的余弦值.