题目内容
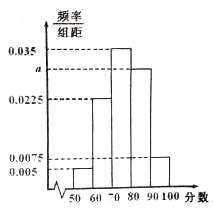
某校高三年级一次数学考试后,为了解学生的数学学习情况,随机抽取 名学生的数学成绩,制成表所示的频率分布表.
名学生的数学成绩,制成表所示的频率分布表.
| 组号 | 分组 | 频数 | 频率 |
| 第一组 |  |  |  |
| 第二组 |  |  |  |
| 第三组 |  |  |  |
| 第四组 |  | 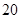 |  |
| 第五组 |  |  |  |
| 合计 |  |  | |
 、
、 、
、 的值;
的值;(2)若从第三、四、五组中用分层抽样方法抽取
 名学生,并在这
名学生,并在这 名学生中随机抽取
名学生中随机抽取 名学生与张老师面谈,求第三组中至少有
名学生与张老师面谈,求第三组中至少有 名学生与张老师面谈的概率
名学生与张老师面谈的概率
(1)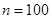 ,
,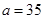 ,
,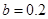 ;(2)
;(2)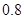 .
.
解析试题分析:(1)先根据相应组的频数除以样本总容量等于相应组的频率列式求出 、
、 、
、 的值;(2)先利用分成抽样的方法确定从第三、四、五组抽取的人数,并将从每组抽取的人进行编号,利用列举法将所有的基本事件列举出,并确定基本事件总数,然后确定问题中设计事件的基本事件及其数目,利用古典概型的概率计算公式求出相应事件的概率.
的值;(2)先利用分成抽样的方法确定从第三、四、五组抽取的人数,并将从每组抽取的人进行编号,利用列举法将所有的基本事件列举出,并确定基本事件总数,然后确定问题中设计事件的基本事件及其数目,利用古典概型的概率计算公式求出相应事件的概率.
试题解析:(1)依题意,得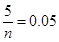 ,
,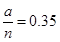 ,
,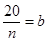 ,
,
解得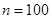 ,
,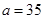 ,
,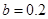 ;
;
(2)因为第三、四、五组共有 名学生,用分层抽样的方法抽取
名学生,用分层抽样的方法抽取 名学生,
名学生,
则第三、四、五组分别抽取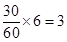 名,
名, 名,
名, 名.
名.
第三组的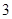 名学生记为
名学生记为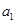 、
、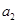 、
、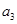 ,第四组的
,第四组的 名学生记为
名学生记为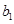 、
、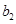 ,第五组的
,第五组的 名学生记为
名学生记为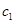 ,
,
则从 名学生中随机抽取
名学生中随机抽取 名,共有
名,共有 种不同取法,具体如下:
种不同取法,具体如下: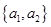 ,
,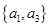 ,
,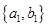 ,
,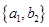 ,
,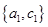 ,
, ,
,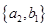 ,
, ,
,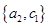 ,
,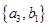 ,
,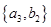 ,
,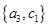 ,
, ,
,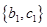 ,
,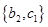 ,
,
其中第三组的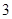 名学生
名学生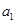 、
、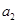 、
、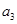 没有一名学生被抽取的情况有
没有一名学生被抽取的情况有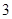 种,具体如下:
种,具体如下: 、
、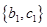 、
、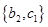 ,
,
故第三组中至少有 名学生与张老师面谈的概率为
名学生与张老师面谈的概率为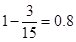 .
.
考点:1.分层抽样;2.古典概型

练习册系列答案
相关题目
为了了解调研高一年级新学生的智力水平,某校按l 0%的比例对700名高一学生按性别分别进行“智力评分”抽样检查,测得“智力评分”的频数分布表如下表l,表2.
表1:男生“智力评分”频数分布表
| 智力评分 | 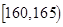 | 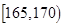 | 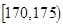 | 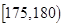 | 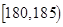 | 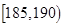 |
| 频数 | 2 | 5 | 14 | 13 | 4 | 2 |
表2:女生“智力评分”频数分布表
| 智力评分 | 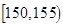 | 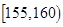 | 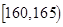 | 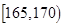 | 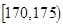 | 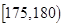 |
| 频数 | 1 | 7 | 12 | 6 | 3 | 1 |
(1)求高一的男生人数并完成下面男生的频率分布直方图;
(2)估计该校学生“智力评分”在[1 65,1 80)之间的概率;
(3)从样本中“智力评分”在[180,190)的男生中任选2人,求至少有1人“智力评分”在[185,190)之间的概率.
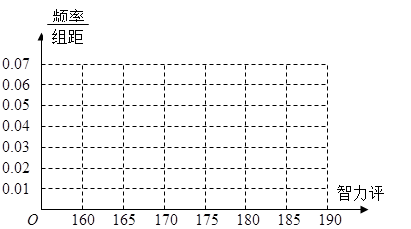
户外运动已经成为一种时尚运动,某单位为了了解员工喜欢户外运动是否与性别有关,决定从本单位全体650人中采用分层抽样的办法抽取50人进行问卷调查,得到了如下列联表:
| | 喜欢户外运动 | 不喜欢户外运动 | 合计 |
| 男性 | | 5 | |
| 女性 | 10 | | |
| 合计 | | | 50 |
 .
.(1)请将上面的列联表补充完整;(2)求该公司男、女员工各多少名;
(3)是否有
 的把握认为喜欢户外运动与性别有关?并说明你的理由.
的把握认为喜欢户外运动与性别有关?并说明你的理由.下面的临界值表仅供参考:
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
 ,其中
,其中 .
.  元/张
元/张 ,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少
,则“足球迷”中非“铁杆足球迷”愿意前往观看的人数会减少 ,“铁杆足球迷”愿意前往观看的人数会减少
,“铁杆足球迷”愿意前往观看的人数会减少 .问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
.问票价至少定为多少元/张时,才能使前往现场观看足球比赛的人数不超过10万人?
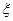 的分布列与期望.
的分布列与期望.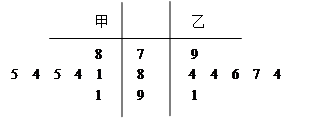
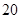 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于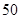 公里和
公里和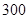 公里之间,将统计结果分
公里之间,将统计结果分 组:
组: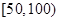 ,
,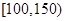 ,
,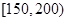 ,
,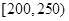 ,
, ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.
 的值;
的值;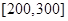 的车辆数;
的车辆数;