题目内容
6.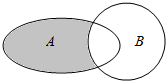 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )| A. | {x|-2<x≤1} | B. | {x|-1<x≤2} | C. | {x|-1<x<1} | D. | {x|-1<x≤1} |
分析 根据Venn图和集合之间的关系进行判断.
解答 解:由Venn图可知,阴影部分的元素为属于A当不属于B的元素构成,所以用集合表示为A∩(∁UB).
A={x|x2-2x-3<0}={x|-1<x<3},
当x<0时,由f(x)>1得($\frac{1}{3}$)x-8>1,即($\frac{1}{3}$)x>9,即3-x>9,则-x>2,即x<-2.
当x≥0时,由f(x)>1得x2+x-1>1,即x2+x-2>0,得x>1或x<-2,则x>1.
即B={x|x>1或x<-2},
则∁UB={x|-2≤x≤1},
则A∩(∁UB)={x|-1<x≤1},
故选:D.
点评 本题主要考查Venn图表达 集合的关系和运算,比较基础.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
17.已知函数f(x)=$\left\{\begin{array}{l}{2|x-2|-1}&{1≤x≤3}\\{\frac{1}{2}f(\frac{x}{3})}&{x>3}\end{array}\right.$,则方程f(x)=$\frac{1}{2}$的解的个数为( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 4个以上 |
11.直线a(x+y-3)+b(x-y+1)=0与圆x2+y2=5的位置关系是( )
| A. | 相交 | B. | 相切 | C. | 相离 | D. | 以上均不对 |