题目内容
18.△ABC所在平面内有一点O,满足2$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=0,过点O的直线分别交AB,AC于点M,N,且$\overrightarrow{AM}$=λ$\overrightarrow{AB}$,$\overrightarrow{AN}$=$\frac{2}{3}$$\overrightarrow{AC}$,则λ=$\frac{2}{5}$.分析 根据M,O,N三点共线,便有$\overrightarrow{MO}=k\overrightarrow{MN}$,从而$\overrightarrow{MA}+\overrightarrow{AO}=k(\overrightarrow{MA}+\overrightarrow{AN})$,这样带入$\overrightarrow{AM}=λ\overrightarrow{AB},\overrightarrow{AN}=\frac{2}{3}\overrightarrow{AC}$便可得到,$\overrightarrow{AO}=(1-k)λ(\overrightarrow{OB}-\overrightarrow{OA})$$+\frac{2k}{3}(\overrightarrow{OC}-\overrightarrow{OA})$,这样可以解出$\overrightarrow{CO}=\frac{(k-1)λ-\frac{2k}{3}+1}{\frac{2k}{3}}\overrightarrow{OA}$$+\frac{(1-k)λ}{\frac{2k}{3}}\overrightarrow{OC}$,而根据条件知,$\overrightarrow{CO}=2\overrightarrow{OA}+\overrightarrow{OB}$,这样便可由平面向量基本定理得到$\left\{\begin{array}{l}{\frac{(k-1)λ-\frac{2k}{3}+1}{\frac{2k}{3}}=2}\\{\frac{(1-k)λ}{\frac{2k}{3}}=1}\end{array}\right.$,解该方程即可得出λ的值.
解答  解:如图,M,O,N三点共线,所以:
解:如图,M,O,N三点共线,所以:
$\overrightarrow{MO}=k\overrightarrow{MN}$,k∈R;
∴$\overrightarrow{MA}+\overrightarrow{AO}=k(\overrightarrow{MA}+\overrightarrow{AN})$;
∴$\overrightarrow{AO}=(1-k)\overrightarrow{AM}+k\overrightarrow{AN}$=$(1-k)λ\overrightarrow{AB}+\frac{2k}{3}\overrightarrow{AC}$=$(1-k)λ(\overrightarrow{OB}-\overrightarrow{OA})+\frac{2k}{3}(\overrightarrow{OC}-\overrightarrow{OA})$;
∴$[(k-1)λ-\frac{2k}{3}+1]\overrightarrow{OA}$$+(1-k)λ\overrightarrow{OB}+\frac{2k}{3}\overrightarrow{OC}=\overrightarrow{0}$;
∴$\overrightarrow{CO}=\frac{(k-1)λ-\frac{2k}{3}+1}{\frac{2k}{3}}\overrightarrow{OA}+\frac{(1-k)λ}{\frac{2k}{3}}\overrightarrow{OB}$;
又由$2\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=\overrightarrow{0}$;
∴$\overrightarrow{CO}=2\overrightarrow{OA}+\overrightarrow{OB}$;
∴由平面向量基本定理得,$\left\{\begin{array}{l}{\frac{(k-1)λ-\frac{2k}{3}+1}{\frac{2k}{3}}=2}\\{\frac{(1-k)λ}{\frac{2k}{3}}=1}\end{array}\right.$;
解得:$k=\frac{3}{8}$,$λ=\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 考查共线向量基本定理,平面向量基本定理,以及向量加法、减法的几何意义,向量的数乘运算.

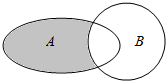 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )| A. | {x|-2<x≤1} | B. | {x|-1<x≤2} | C. | {x|-1<x<1} | D. | {x|-1<x≤1} |
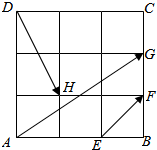 在如图所示的图形中,每个小四边形都是边长相等的正方形,则向量$\overrightarrow{AG}$=( )
在如图所示的图形中,每个小四边形都是边长相等的正方形,则向量$\overrightarrow{AG}$=( )| A. | $\frac{2}{3}\overrightarrow{EF}+\frac{7}{3}\overrightarrow{DH}$ | B. | $\frac{5}{3}\overrightarrow{EF}+\frac{4}{3}\overrightarrow{DH}$ | C. | $\frac{8}{3}\overrightarrow{EF}+\frac{1}{3}\overrightarrow{DH}$ | D. | $\frac{10}{3}\overrightarrow{EF}-\frac{1}{3}\overrightarrow{DH}$ |
| A. | ab∈A | B. | ab∈B | C. | ab∈A且ab∈B |