题目内容
15.设函数f(x)=cos2x+$\frac{1}{2}$sin(2x+$\frac{π}{2}$)-$\frac{1}{2}$.(1)求f(x)在($\frac{π}{6}$,$\frac{2π}{3}$)上的值域.
(2)设A,B,C为△ABC的三个内角,若角C满足f($\frac{C}{2}$)=$\frac{\sqrt{2}}{2}$,且边c=$\sqrt{2}$a,求角A.
分析 (1)由条件利用三角函数的恒等变换化简f(x)的解析式,再根据余弦函数的定义域和值域,求得f(x)在($\frac{π}{6}$,$\frac{2π}{3}$)上的值域
(2)由条件求得cosC=$\frac{\sqrt{2}}{2}$,可得 C=$\frac{π}{4}$.再利用正弦定理求得sinA的值,可得A的值.
解答 解:(1)∵函数f(x)=cos2x+$\frac{1}{2}$sin(2x+$\frac{π}{2}$)-$\frac{1}{2}$=$\frac{1}{2}$cos2x+$\frac{1}{2}$cos2x=cos2x,
故当x∈($\frac{π}{6}$,$\frac{2π}{3}$)时,2x∈($\frac{π}{3}$,$\frac{4π}{3}$),cos2x∈[-1,$\frac{1}{2}$).
(2)△ABC中,∵f($\frac{C}{2}$)=cosC=$\frac{\sqrt{2}}{2}$,∴C=$\frac{π}{4}$.
又c=$\sqrt{2}$a,由正弦定理可得$\frac{c}{a}$=$\frac{\frac{\sqrt{2}}{2}}{sinA}$=$\sqrt{2}$,求得sinA=$\frac{1}{2}$,∴A=$\frac{π}{6}$ 或A=$\frac{5π}{6}$(舍去)
综上,A=$\frac{π}{3}$.
点评 本题主要考查三角函数的恒等变换,余弦函数的定义域和值域,正弦定理的应用,根据三角函数的值求角,属于中档题.

练习册系列答案
相关题目
5.设F(x)=f(x)+f(-x),x∈R,若[-π,-$\frac{π}{2}$]是函数F(x)的单调递增区间,则一定是F(x)单调递减区间的是( )
| A. | [-$\frac{π}{2}$,0] | B. | [$\frac{π}{2}$,0] | C. | [π,$\frac{3}{3}$π] | D. | [$\frac{3}{2}π$,2π] |
6.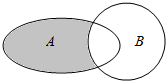 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )| A. | {x|-2<x≤1} | B. | {x|-1<x≤2} | C. | {x|-1<x<1} | D. | {x|-1<x≤1} |
7.集合A={x|x=3m+1,m∈Z},B={x|x=3n+1,n∈Z},若a∈A,b∈B,则有( )
| A. | ab∈A | B. | ab∈B | C. | ab∈A且ab∈B |