题目内容
17.已知函数f(x)=$\left\{\begin{array}{l}{2|x-2|-1}&{1≤x≤3}\\{\frac{1}{2}f(\frac{x}{3})}&{x>3}\end{array}\right.$,则方程f(x)=$\frac{1}{2}$的解的个数为( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 4个以上 |
分析 利用函数f(x)=$\left\{\begin{array}{l}{2|x-2|-1}&{1≤x≤3}\\{\frac{1}{2}f(\frac{x}{3})}&{x>3}\end{array}\right.$,结合方程f(x)=$\frac{1}{2}$,即可得出结论.
解答 解:1≤x≤3时,f(x)=$\left\{\begin{array}{l}{3-2x,1≤x≤2}\\{2x-5,2<x≤3}\end{array}\right.$,
3<x≤6时,1<$\frac{x}{3}$≤2,f($\frac{x}{3}$)=3-$\frac{2}{3}$x,f(x)=$\frac{1}{2}$f($\frac{x}{3}$)=$\frac{3}{2}$-$\frac{1}{3}$x;
6<x≤9时,2<$\frac{x}{3}$≤3,f($\frac{x}{3}$)=$\frac{2}{3}$x-5,f(x)=$\frac{1}{2}$f($\frac{x}{3}$)=$\frac{1}{3}$x-$\frac{5}{2}$;
∴1≤x≤2时,3-2x=$\frac{1}{2}$,x=$\frac{5}{4}$;
2<x≤3时,2x-5=$\frac{1}{2}$,x=$\frac{11}{4}$;
6<x≤9时,$\frac{1}{3}$x-$\frac{5}{2}$=$\frac{1}{2}$,x=9,
故选:B.
点评 本题考查方程f(x)=$\frac{1}{2}$的解的个数,考查分段函数,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
5.设F(x)=f(x)+f(-x),x∈R,若[-π,-$\frac{π}{2}$]是函数F(x)的单调递增区间,则一定是F(x)单调递减区间的是( )
| A. | [-$\frac{π}{2}$,0] | B. | [$\frac{π}{2}$,0] | C. | [π,$\frac{3}{3}$π] | D. | [$\frac{3}{2}π$,2π] |
2.关于x的不等式kx2-2x+1>0的解集是{x∈R|x≠$\frac{1}{k}$},则k的值是( )
| A. | 1 | B. | -1 | C. | ±1 | D. | -1≤x≤1 |
9.把幂函数y=x-2向左平移2个单位后的函数为 ( )
| A. | y=x-2-2 | B. | y=x-2+2 | C. | y=(x-2)-2 | D. | y=(x+2)-2 |
6.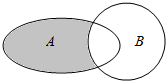 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
 已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )
已知全集U=R,函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{x}-8(x<0)}\\{{x}^{2}+x-1(x≥0)}\end{array}\right.$,集合A={x|x2-2x<3},B={x|f(x)>1},则图中阴影部分所表示的集合为( )| A. | {x|-2<x≤1} | B. | {x|-1<x≤2} | C. | {x|-1<x<1} | D. | {x|-1<x≤1} |