题目内容
对某种赌博游戏调查后,发现其规则如下:摊主在口袋中装入8枚黑色和8枚白色的围棋子,参加者从中随意一次摸出5枚,摸一次交手续费2元,而中彩情况如下:
现在我们试计算如下问题:
(1)求一次获得20元彩金的概率;(结果用最简分数表示)
(2)分别求一次获3元和纪念奖的概率;(结果用最简分数表示)
(3)如果某天有1000次摸奖,估计摊主是赔钱还是挣钱?大概是多少元?
| 摸子情况 | 5枚白 | 4枚白 | 3枚白 | 其它 |
| 彩金 | 20元 | 3元 | 纪念品价值1元 | 无奖同乐一次 |
(1)求一次获得20元彩金的概率;(结果用最简分数表示)
(2)分别求一次获3元和纪念奖的概率;(结果用最简分数表示)
(3)如果某天有1000次摸奖,估计摊主是赔钱还是挣钱?大概是多少元?
考点:古典概型及其概率计算公式,相互独立事件的概率乘法公式
专题:概率与统计
分析:(1)由题意可得总的基本事件共
种,一次获得20元彩金需5枚全白共
种,由概率公式可得;
(2)同(1)的求法易得一次中奖3元彩金的概率和中纪念奖概率;
(3)1000次收手续费2000元,减去支付的三部分可得.
| C | 5 16 |
| C | 5 8 |
(2)同(1)的求法易得一次中奖3元彩金的概率和中纪念奖概率;
(3)1000次收手续费2000元,减去支付的三部分可得.
解答:
解:(1)由题意可得总的基本事件共
种,
一次获得20元彩金需5枚全白共
种,
∴一次摸奖中20元彩金的概率P20=
=
,
(2)同(1)易得一次中奖3元彩金的概率P3=
=
,
而中纪念奖概率P纪=
=
,
(3)摊主赔钱还是挣钱由其支付完奖金后的余额决定,1000次收手续费2000元.
预计支付20元奖需m20=
×1000×20元;
支付3元奖需m3=
×1000×3元
支付纪念奖需m纪=
×1000×1元,
∴余额m=2000-m20-m3-m纪=1000元
答:一次获得20元彩金的概率为
;一次获3元的概率为
,一次获纪念奖的概率为
;摊主大概挣钱1000元.
| C | 5 16 |
一次获得20元彩金需5枚全白共
| C | 5 8 |
∴一次摸奖中20元彩金的概率P20=
| ||
|
| 1 |
| 78 |
(2)同(1)易得一次中奖3元彩金的概率P3=
| ||||
|
| 5 |
| 39 |
而中纪念奖概率P纪=
| ||||
|
| 14 |
| 39 |
(3)摊主赔钱还是挣钱由其支付完奖金后的余额决定,1000次收手续费2000元.
预计支付20元奖需m20=
| 1 |
| 78 |
支付3元奖需m3=
| 5 |
| 39 |
支付纪念奖需m纪=
| 14 |
| 39 |
∴余额m=2000-m20-m3-m纪=1000元
答:一次获得20元彩金的概率为
| 1 |
| 78 |
| 5 |
| 39 |
| 14 |
| 39 |
点评:本题考查古典概型及其概率公式,属基础题.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
sin515°•cos35°-cos25°•cos235°的值为( )
A、-
| ||||
B、
| ||||
C、
| ||||
D、-
|
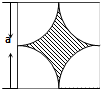 如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为
如图所示,墙上挂有边长为a的正方形木板,它的四个角的空白部分都是以正方形的顶点为圆心,半径为| a |
| 2 |
A、
| ||
B、1-
| ||
C、1-
| ||
| D、与a的取值有关 |
若数列{an}满足
-
=d(n∈Nn,d为常数),则称数列{an}为“调和数列”.已知数列{
}为“调和数列”,且x1+x2+…+x20=200,则x3•x18的最大值为( )
| 1 |
| an+1 |
| 1 |
| an |
| 1 |
| xn |
| A、50 | B、100 |
| C、150 | D、200 |
数列{an}满足a1=2,an+1=-
,则a2008=( )
| 1 |
| an+1 |
| A、2 | ||
B、-
| ||
C、-
| ||
| D、1 |
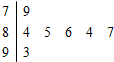 如图是2012年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )
如图是2012年元旦晚会举办的挑战主持人大赛上,七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的众数和中位数分别为( )| A、85,84 |
| B、84,84 |
| C、84,85 |
| D、85,85 |