题目内容
(本小题11分)已知函数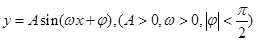 相邻的两个最高点和最低点分别为
相邻的两个最高点和最低点分别为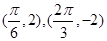
(1)求函数表达式;
(2)求该函数的单调递减区间;
(3)求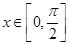 时,该函数的值域
时,该函数的值域
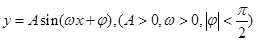 相邻的两个最高点和最低点分别为
相邻的两个最高点和最低点分别为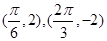
(1)求函数表达式;
(2)求该函数的单调递减区间;
(3)求
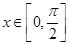 时,该函数的值域
时,该函数的值域(1) ;(2)单调增区间为
;(2)单调增区间为 ;(3)
;(3) 。
。
 ;(2)单调增区间为
;(2)单调增区间为 ;(3)
;(3) 。
。本试题主要是考查了三角函数图形与性质的运用。
(1)由函数图象过最高点的坐标可得
相邻的最值点的横坐标为半个周期,即 ,得
,得
又 ,所以w=2,然后当
,所以w=2,然后当 ,代入得到初相的值,进而解得。
,代入得到初相的值,进而解得。
(2)因为
解得: ,解得单调区间。
,解得单调区间。
(3)因为当 时,该函数为增函数,
时,该函数为增函数,
当 时,该函数为减函数,那么可知在给定区间的最大值问题和最小值得到值域。
时,该函数为减函数,那么可知在给定区间的最大值问题和最小值得到值域。
解:(1)由函数图象过最高点的坐标可得 (1分)
(1分)
相邻的最值点的横坐标为半个周期,即 ,得
,得
又 ,所以
,所以 , (1分)
, (1分)
所以 ,当
,当
得 ,即
,即 (1分)
(1分)
所以 ,由
,由 ,得
,得 (1分)
(1分)
所以 (1分)
(1分)
(2) (1分)
(1分)
解得: (1分)
(1分)
即该函数的单调增区间为 (1分)
(1分)
(3)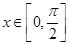
当 时,该函数为增函数,
时,该函数为增函数,
当 时,该函数为减函数, (1分)
时,该函数为减函数, (1分)
所以当 时,
时, ,当
,当 时,
时, (1分)
(1分)
所以该函数的值域为 (1分)
(1分)
(1)由函数图象过最高点的坐标可得

相邻的最值点的横坐标为半个周期,即
 ,得
,得
又
 ,所以w=2,然后当
,所以w=2,然后当 ,代入得到初相的值,进而解得。
,代入得到初相的值,进而解得。(2)因为

解得:
 ,解得单调区间。
,解得单调区间。(3)因为当
 时,该函数为增函数,
时,该函数为增函数, 当
 时,该函数为减函数,那么可知在给定区间的最大值问题和最小值得到值域。
时,该函数为减函数,那么可知在给定区间的最大值问题和最小值得到值域。解:(1)由函数图象过最高点的坐标可得
 (1分)
(1分)相邻的最值点的横坐标为半个周期,即
 ,得
,得
又
 ,所以
,所以 , (1分)
, (1分)所以
 ,当
,当
得
 ,即
,即 (1分)
(1分)所以
 ,由
,由 ,得
,得 (1分)
(1分)所以
 (1分)
(1分)(2)
 (1分)
(1分)解得:
 (1分)
(1分)即该函数的单调增区间为
 (1分)
(1分)(3)
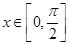
当
 时,该函数为增函数,
时,该函数为增函数, 当
 时,该函数为减函数, (1分)
时,该函数为减函数, (1分)所以当
 时,
时, ,当
,当 时,
时, (1分)
(1分)所以该函数的值域为
 (1分)
(1分)
练习册系列答案
相关题目
 .
. 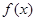 的最小正周期和当
的最小正周期和当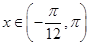 时的值域;
时的值域; 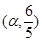 ,
,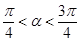 .求
.求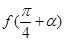 的值.
的值.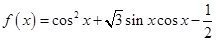
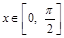 求
求 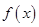 的最小值及取得最小值时相应的x的值;
的最小值及取得最小值时相应的x的值;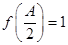 ,b=l,c=4,求a的值.
,b=l,c=4,求a的值. ,且
,且 ,
, 的取值范围;
的取值范围; ;
; 的取值范围.
的取值范围.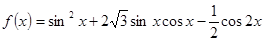 ,
,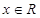 。
。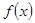 的最小正周期和值域;
的最小正周期和值域;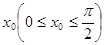 为
为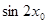 的值。
的值。
 的值;
的值; 的最大值和最小值。
的最大值和最小值。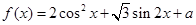 (a∈R,a为常数).
(a∈R,a为常数).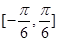 上最大值与最小值之和为3,求a的值;
上最大值与最小值之和为3,求a的值; 为坐标原点,向量
为坐标原点,向量 ,点
,点 是直线
是直线 上的一点,且点
上的一点,且点 分有向线段
分有向线段 的比为
的比为 .
.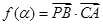 ,
, ,讨论函数
,讨论函数 的单调性,并求其值域;
的单调性,并求其值域; 三点共线,求
三点共线,求 的值.
的值. ,且
,且 =
= 则( )
则( ) ≤
≤ ≤
≤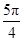

 ≤
≤