题目内容
已知向量 ,且
,且 ,
,
⑴ 的取值范围;
的取值范围;
⑵ ⑵求证 ;
;
⑶ ⑶求函数 的取值范围.
的取值范围.
 ,且
,且 ,
,⑴
 的取值范围;
的取值范围;⑵ ⑵求证
 ;
;⑶ ⑶求函数
 的取值范围.
的取值范围.解:(1)∵ =sinx·cosx+sinx·cosx
=sinx·cosx+sinx·cosx
=2sinx·cosx=sin2x (2’) x∈
∴2x∈
∴ ∈ (4’) ………4分
∈ (4’) ………4分
(2)证明:∵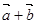 ="(cos+sinx," sinx+cosx)
="(cos+sinx," sinx+cosx)
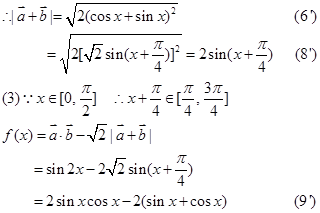
………10分
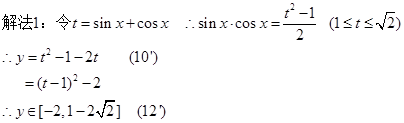 ………14分
………14分
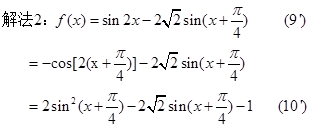
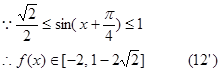 ………14分
………14分
 =sinx·cosx+sinx·cosx
=sinx·cosx+sinx·cosx=2sinx·cosx=sin2x (2’) x∈
∴2x∈
∴
 ∈ (4’) ………4分
∈ (4’) ………4分(2)证明:∵
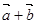 ="(cos+sinx," sinx+cosx)
="(cos+sinx," sinx+cosx)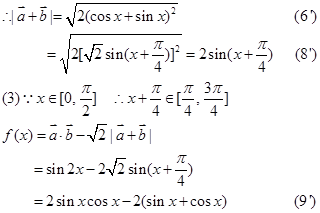
………10分
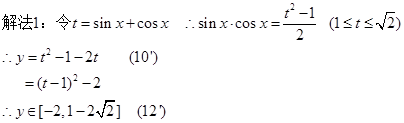 ………14分
………14分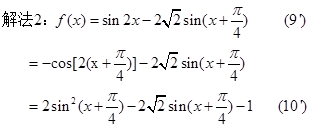
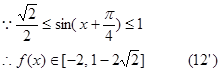 ………14分
………14分本试题主要是考查了向量的数量积和三角函数性质的综合运用问题。
(1)根据已知的向量的坐标表示向量的数量积,得到关于x的三角函数,结合三角函数的性质得到范围。
(2)利用向量的平方就是向量模的平方的关系得到
(3)利用二倍角公式化简变形得到单一三角函数,然后求解值域。
(1)根据已知的向量的坐标表示向量的数量积,得到关于x的三角函数,结合三角函数的性质得到范围。
(2)利用向量的平方就是向量模的平方的关系得到
(3)利用二倍角公式化简变形得到单一三角函数,然后求解值域。

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
 (
( )的图象上所有点向左平行移动
)的图象上所有点向左平行移动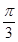 个单位长度,再把所得图象上所有点的横坐标缩短到原来的
个单位长度,再把所得图象上所有点的横坐标缩短到原来的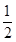 倍(纵坐标不变),得到的图象所表示的函数的解析式是( )
倍(纵坐标不变),得到的图象所表示的函数的解析式是( ) ,
, ,
, ,
,  ,
, 


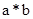 为:
为: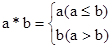 ,例如1*2=1,2*1=1,设函数
,例如1*2=1,2*1=1,设函数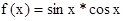 则函数
则函数 的最小正周期为_______,使
的最小正周期为_______,使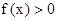 成立的集合为__________________________
成立的集合为__________________________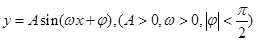 相邻的两个最高点和最低点分别为
相邻的两个最高点和最低点分别为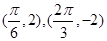
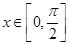 时,该函数的值域
时,该函数的值域 上的函数
上的函数 的图像关于直线
的图像关于直线 对称,当
对称,当 时,函数
时,函数
 的图像如下图所示。
的图像如下图所示。
 上的解析式;
上的解析式; 的解.
的解.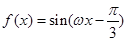
 和
和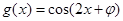 的图象的对称中心完全相同,若
的图象的对称中心完全相同,若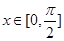 ,则
,则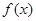 的最小值是
的最小值是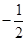 B.
B.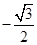 C.
C.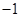 D.
D.
 的图象关于直线
的图象关于直线 对称,那么
对称,那么 ( )
( ) B -
B -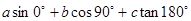 的值为 .
的值为 .