题目内容
【题目】某次数学测试之后,数学组的老师对全校数学总成绩分布在[105,135)的n名同学的19题成绩进行了分析,数据整理如下:
组数 | 分组 | 19题满分人数 | 19题满分人数占本组人数比例 |
第一组 | [105,110] | 15 | 0.3 |
第二组 | [110,115) | 30 | 0.3 |
第三组 | [115,120) | x | 0.4 |
第四组 | [120,125) | 100 | 0.5 |
第五组 | [125,130) | 120 | 0.6 |
第六组 | [130,135) | 195 | y |
(Ⅰ)补全所给的频率分布直方图,并求n,x,y的值;
(Ⅱ)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,并从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,求随机变量ξ的分布列及期望.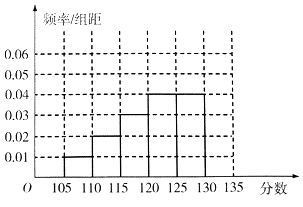
【答案】解:(I)由第一组[105,110)可得: ![]() =0.3,解得:n=1000. ∴
=0.3,解得:n=1000. ∴ ![]() =0.4,解得:x=60.
=0.4,解得:x=60.
在区间[1305,135)的频率为z,则(0.01+0.02+0.03+0.04×2+z)×5=1,解得z=0.06.
∴ ![]() =y,解得y=0.65.
=y,解得y=0.65.
(II)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,
则分别抽取3,6份.
从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,取值为:0,1,2.
则P(ξ=k)= ![]() ,可得P(ξ=0)=
,可得P(ξ=0)= ![]() ,P(ξ=1)=
,P(ξ=1)= ![]() ,P(ξ=2)=
,P(ξ=2)= ![]() =
= ![]() .
.
ξ的分布列为:
ξ | 0 | 1 | 2 |
P |
|
|
|
E(ξ)=0+1× ![]() +2×
+2× ![]() =
= ![]()
【解析】(I)利用频率分布直方图的性质即可得出.(II)现从[110,115)、[115,120)两个分数段的19题满分的试卷中,按分层抽样的方法抽取9份进行展出,则分别抽取3,6份.从9份试卷中选出两份作为优秀试卷,优秀试卷在[115,120)中的分数记为ξ,取值为:0,1,2.利用P(ξ=k)= ![]() 即可得出.
即可得出.
【考点精析】认真审题,首先需要了解频率分布直方图(频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息),还要掌握离散型随机变量及其分布列(在射击、产品检验等例子中,对于随机变量X可能取的值,我们可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.离散型随机变量的分布列:一般的,设离散型随机变量X可能取的值为x1,x2,.....,xi,......,xn,X取每一个值 xi(i=1,2,......)的概率P(ξ=xi)=Pi,则称表为离散型随机变量X 的概率分布,简称分布列)的相关知识才是答题的关键.

【题目】调查表明:甲种农作物的长势与海拔高度、土壤酸碱度、空气湿度的指标有极强的相关性,现将这三项的指标分别记为x,y,z,并对它们进行量化:0表示不合格,1表示临界合格,2表示合格,再用综合指标ω=x+y+z的值评定这种农作物的长势等级,若ω≥4,则长势为一级;若2≤ω≤3,则长势为二级;若0≤ω≤1,则长势为三级,为了了解目前这种农作物长势情况,研究人员随机抽取10块种植地,得到如表中结果:
种植地编号 | A1 | A2 | A3 | A4 | A5 |
(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (0,0,1) | (1,2,1) |
种植地编号 | A6 | A7 | A8 | A9 | A10 |
(x,y,z) | (1,1,2) | (1,1,1) | (1,2,2) | (1,2,1) | (1,1,1) |
(Ⅰ)在这10块该农作物的种植地中任取两块地,求这两块地的空气湿度的指标z相同的概率;
(Ⅱ)从长势等级是一级的种植地中任取一块地,其综合指标为A,从长势等级不是一级的种植地中任取一块地,其综合指标为B,记随机变量X=A﹣B,求X的分布列及其数学期望.
【题目】某中学拟在高一下学期开设游泳选修课,为了了解高一学生喜欢游泳是否与性别有关,该学校对100名高一新生进行了问卷调查,得到如下列联表:
喜欢游泳 | 不喜欢游泳 | 合计 | |
男生 | 10 | ||
女生 | 20 | ||
合计 |
已知在这100人中随机抽取1人抽到喜欢游泳的学生的概率为 ![]() .
.
下面的临界值表仅供参考:
P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
(1)请将上述列联表补充完整:并判断是否有99.9%的把握认为喜欢游泳与性别有关?并说明你的理由;
(2)针对于问卷调查的100名学生,学校决定从喜欢游泳的人中按分层抽样的方法随机抽取6人成立游泳科普知识宣传组,并在这6人中任选2人作为宣传组的组长,设这两人中男生人数为X,求X的分布列和数学期望.