题目内容
已知抛物线C1:x2=2y的焦点为F,以F为圆心的圆C2交C1于A,B,交C1的准线于C,D,若四边形ABCD是矩形,则圆C2的方程为( )
A.x2+(y-
| B.x2+(y-
| C.x2+(y-1)2=12 | D.x2+(y-1)2=16 |
依题意,抛物线C1:x2=2y的焦点为F(0,
),
∴圆C2的圆心坐标为F(0,
),
作图如下:
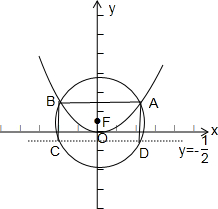
∵四边形ABCD是矩形,且BD为直径,AC为直径,F(0,
)为圆C2的圆心,
∴点F为该矩形的两条对角线的交点,
∴点F到直线CD的距离与点F到AB的距离相等,又点F到直线CD的距离d=1,
∴直线AB的方程为:y=
,
∴A(
,
),
∴圆C2的半径r=|AF|=
=2,
∴圆C2的方程为:x2+(y-
)2=4,
故选:B.
| 1 |
| 2 |
∴圆C2的圆心坐标为F(0,
| 1 |
| 2 |
作图如下:

∵四边形ABCD是矩形,且BD为直径,AC为直径,F(0,
| 1 |
| 2 |
∴点F为该矩形的两条对角线的交点,
∴点F到直线CD的距离与点F到AB的距离相等,又点F到直线CD的距离d=1,
∴直线AB的方程为:y=
| 3 |
| 2 |
∴A(
| 3 |
| 3 |
| 2 |
∴圆C2的半径r=|AF|=
(
|
∴圆C2的方程为:x2+(y-
| 1 |
| 2 |
故选:B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目