Question

  已知数列{a_n}满足条件: a₁=1,a₂=r(r＞0),且{a_na_n+1}是公比为q(q＞0)的等比数列，设b_n=a_2n－1+a_2n(n=1,2,…).

(1)求出使不等式a_na_n+1+a_n+1a_n+2＞a_n+2a_n+3(n∈N^*)成立的q的取值范围；

(2)求b_n和，其中S_n=b₁+b₂+…+b_n；

(3)设r=2^19.2－1，q=，求数列{}的最大项和最小项的值.

Answer 1

(1) 0＜q＜; (2)  (3) {C_n}的最大项C₂₁=2.25，最小项C₂₀=－4

解析:

(1)由题意得rq^n－1+rqⁿ＞rqⁿ⁺¹.

由题设r＞0,q＞0,故从上式可得  q²－q－1＜0，解得＜q＜,因q＞0,故0＜q＜;

(2)∵.

b₁=1+r≠0，所以{b_n}是首项为1+r，公比为q的等比数列，从而b_n=(1+r)q^n-1. 

当q=1时，S_n=n(1+r),

 

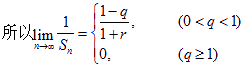
,从上式可知，

当n－20.2＞0，即n≥21(n∈N^*)时，C_n随n的增大而减小，

故1＜C_n≤C₂₁=1+=2.25                   ①

当n－20.2＜0，即n≤20(n∈N^*)时，C_n也随n的增大而减小，

故1＞C_n≥C₂₀=1+=－4                     ②

综合①②两式知，对任意的自然数n有C₂₀≤C_n≤C₂₁,

故{C_n}的最大项C₂₁=2.25，最小项C₂₀=－4。