题目内容
【题目】已知首项为
的等比数列
的前n项和为
, 且
成等差数列.
(Ⅰ) 求数列
的通项公式;
(Ⅱ) 证明
.
【答案】(Ⅰ) 
(Ⅱ)见解析
【解析】(Ⅰ)设等比数列
的公比为
，因为
成等差数列，所以
S4 + 2S2 =4S4 – S3，即
，于是
，又
=
，
所以等比数列
的通项公式为
=.
(Ⅱ)由(Ⅰ)得
，所以
=
，
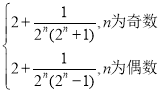当n为奇数时，
随n的增大而减小，所以
=
；
当n为偶数时，随n的增大而增大，所以
=
，
故对于
，有
.
本题第（Ⅰ）问，由S3 + a3, S5 + a5, S4 + a4成等差数列可以求出公比，进而由等比数列的通项公式求出结果；第(Ⅱ)问，先求出
，然后分n为奇数与偶数讨论得出数列
的最大项与最小项的值.对第（Ⅰ）问，要注意细心计算；第二问，注意分n为奇数与偶数两种情况讨论.
阅读快车系列答案【题目】某品牌餐饮公司准备在10个规模相当的地区开设加盟店，为合理安排各地区加盟店的个数，先在其中5个地区试点，得到试点地区加盟店个数分别为1，2，3，4，5时，单店日平均营业额
（万元）的数据如下：
加盟店个数 | 1 | 2 | 3 | 4 | 5 |
单店日平均营业额 | 10.9 | 10.2 | 9 | 7.8 | 7.1 |
（1）求单店日平均营业额（万元）与所在地区加盟店个数
（个）的线性回归方程；
（2）根据试点调研结果，为保证规模和效益，在其他5个地区，该公司要求同一地区所有加盟店的日平均营业额预计值总和不低于35万元，求一个地区开设加盟店个数
的所有可能取值；
（3）小赵与小王都准备加入该公司的加盟店，根据公司规定，他们只能分别从其他五个地区（加盟店都不少于2个）中随机选一个地区加入，求他们选取的地区相同的概率.
（参考数据及公式：
，
，线性回归方程
，其中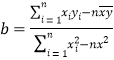
，
.）
【题目】
年，在庆祝中华人民共和国成立
周年之际，又迎来了以“创军人荣耀，筑世界和平”为宗旨的第七届世界军人运动会．据悉，这次军运会将于年
月
日至
日在美丽的江城武汉举行，届时将有来自全世界
多个国家和地区的近万名军人运动员参赛．相对于奥运会、亚运会等大型综合赛事，军运会或许对很多人来说还很陌生．为此，武汉某高校为了在学生中更广泛的推介普及军运会相关知识内容，特在网络上组织了一次“我所知晓的武汉军运会”知识问答比赛，为便于对答卷进行对比研究，组委会抽取了
名男生和名女生的答卷，他们的考试成绩频率分布直方图如下：
（注：问卷满分为分，成绩
的试卷为“优秀”等级）
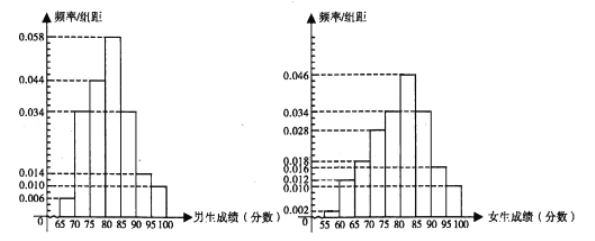
(1)从现有名男生和名女生答卷中各取一份，分别求答卷成绩为“优秀”等级的概率；
(2)求列联表中
，
，
，
的值，并根据列联表回答：能否在犯错误的概率不超过
的前提下认为“答卷成绩为优秀等级与性别有关”？
男 | 女 | 总计 | |
优秀 |
|
|
|
非优秀 |
|
|
|
总计 |
|
|
|
(3)根据男、女生成绩频率分布直方图，对他们的成绩的优劣进行比较．
附：参考公式：
，其中
.
|
|
|
|
|
|
|
|
