题目内容
【题目】已知函数![]() 满足
满足![]() ,若在区间
,若在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,则实数
恰有4个不同的实数解,则实数![]() 的取值范围是___________.
的取值范围是___________.
【答案】![]()
【解析】
由题意,把在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,转化为函数
恰有4个不同的实数解,转化为函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有4个不同的交点,作出函数的图象,结合图象,分类讨论,即可求解,得到答案.
内有4个不同的交点,作出函数的图象,结合图象,分类讨论,即可求解,得到答案.
由题意,函数![]() 满足
满足![]() ,即
,即![]() ,即函数
,即函数![]() 是以6为周期的周期函数,
是以6为周期的周期函数,
又由在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,
恰有4个不同的实数解,
即在区间![]() 内关于
内关于![]() 的方程
的方程![]() 恰有4个不同的实数解,
恰有4个不同的实数解,
即函数![]() 与
与![]() 的图象在区间
的图象在区间![]() 内有4个不同的交点,
内有4个不同的交点,
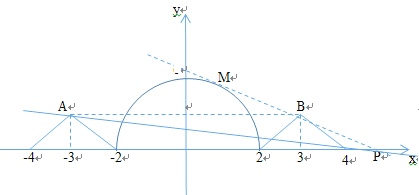
又由函数![]() ,作出函数的图象,如图所示,
,作出函数的图象,如图所示,
由直线![]() ,可知直线恒过点
,可知直线恒过点![]() ,
,
当![]() 时,此时直线
时,此时直线![]() 与函数
与函数![]() 的图象恰有4个交点,
的图象恰有4个交点,
当直线过点![]() 时,此时
时,此时![]() ,即
,即![]() ,此时函数
,此时函数![]() 与直线
与直线![]() 有5个同的交点,
有5个同的交点,
当直线![]() 与半圆
与半圆![]() 相切时,此时圆心到直线
相切时,此时圆心到直线![]() 的距离等于圆的半径,即
的距离等于圆的半径,即![]() ,解得
,解得![]() 或
或![]() (舍去),此时函数
(舍去),此时函数![]() 与直线
与直线![]() 有3个同的交点,
有3个同的交点,
此时函数![]() 与直线
与直线![]() 恰有4个同的交点,则
恰有4个同的交点,则![]()
综上可知,实数![]() 的取值范围是
的取值范围是![]() .
.

 名题金卷系列答案
名题金卷系列答案【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
【题目】下表是某电器销售公司2018年度各类电器营业收入占比和净利润占比统计表:
空调类 | 冰箱类 | 小家电类 | 其它类 | |
营业收入占比 |
|
|
|
|
净利润占比 |
|
|
|
|
则下列判断中不正确的是( )
A. 该公司2018年度冰箱类电器营销亏损
B. 该公司2018年度小家电类电器营业收入和净利润相同
C. 该公司2018年度净利润主要由空调类电器销售提供
D. 剔除冰箱类电器销售数据后,该公司2018年度空调类电器销售净利润占比将会降低