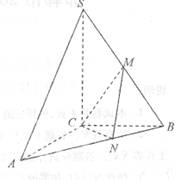
题目内容
如图,三棱锥S-ABC中,△ABC是边长为4的正三角形, ,
, ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.(1)求证:平面SAC⊥平面ABC;
(2)求二面角N-CM-B的一个三角函数值;
(3)求点B到平面CMN的距离.

【答案】分析:(1)取AC中点O,由勾股定理可得SO⊥BO,根据等腰三角形的性质可得SO⊥AC,从而得到SO⊥平面ABC,平面SAC⊥平面ABC.
(2)如图所示建立空间直角坐标系O-xyz,求得平面CMN的一个法向量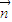 ,平面ABC的一个法向量
,平面ABC的一个法向量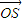 ,可得
,可得
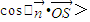 =
=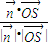 的值,即为所求.
的值,即为所求.
(3)根据点B到平面CMN的距离即为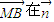 上射影的绝对值
上射影的绝对值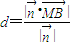 ,求得结果.
,求得结果.
解答: 解:(1)取AC中点O,连接SO,OB,则SO⊥AC,BO⊥AC,
解:(1)取AC中点O,连接SO,OB,则SO⊥AC,BO⊥AC,
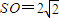 ,
,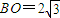 ,
,
∵SO2+BO2=20,SB2=20,∴SO2+BO2=SB2,∴SO⊥BO,
又SO⊥AC,∴SO⊥平面ABC,
∵SO?平面SAC,∴平面SAC⊥平面ABC.
(2)如图所示建立空间直角坐标系O-xyz.
则A(2,0,0),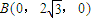 ,C(-2,0,0),
,C(-2,0,0),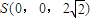 ,
,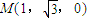 ,
,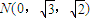 (6分)
(6分)
∵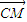 =(3,
=(3,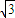 ,0),
,0),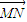 =(-1,0,
=(-1,0,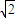 ).
).
设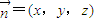 为平面CMN的一个法向量,则
为平面CMN的一个法向量,则
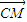 •
•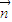 =
=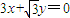 ,
,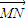 •
•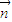 =
=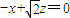 ,
,
取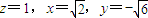 ,∴
,∴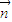 =(
=(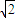 ,-
,-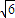 ,1),
,1),
又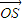 =(0,0,2
=(0,0,2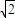 )为平面ABC的一个法向量,
)为平面ABC的一个法向量,
∴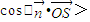 =
=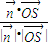 =
= .
.
由图知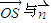 的夹角即为二面角N-CM-B的大小,其余弦值为
的夹角即为二面角N-CM-B的大小,其余弦值为 .
.
(3)由(2)得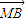 =(-1,
=(-1,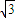 ,0),
,0),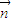 =(
=(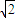 ,-
,-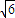 ,1)为平面CMN的一个法向量,
,1)为平面CMN的一个法向量,
∴点B到平面CMN的距离即为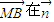 上射影的绝对值
上射影的绝对值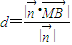 =
=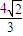 .
.
点评:本题考查证明面面垂直的方法,求二面角的大小,点到平面的距离,求平面的法向量的坐标是解题的关键和易错点.
(2)如图所示建立空间直角坐标系O-xyz,求得平面CMN的一个法向量
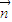 ,平面ABC的一个法向量
,平面ABC的一个法向量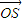 ,可得
,可得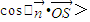 =
=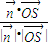 的值,即为所求.
的值,即为所求.(3)根据点B到平面CMN的距离即为
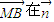 上射影的绝对值
上射影的绝对值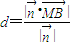 ,求得结果.
,求得结果.解答:
 解:(1)取AC中点O,连接SO,OB,则SO⊥AC,BO⊥AC,
解:(1)取AC中点O,连接SO,OB,则SO⊥AC,BO⊥AC,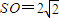 ,
,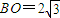 ,
,∵SO2+BO2=20,SB2=20,∴SO2+BO2=SB2,∴SO⊥BO,
又SO⊥AC,∴SO⊥平面ABC,
∵SO?平面SAC,∴平面SAC⊥平面ABC.
(2)如图所示建立空间直角坐标系O-xyz.
则A(2,0,0),
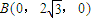 ,C(-2,0,0),
,C(-2,0,0),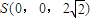 ,
,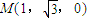 ,
,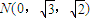 (6分)
(6分)∵
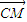 =(3,
=(3,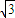 ,0),
,0),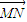 =(-1,0,
=(-1,0,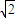 ).
).设
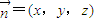 为平面CMN的一个法向量,则
为平面CMN的一个法向量,则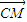 •
•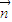 =
=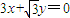 ,
,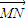 •
•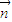 =
=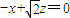 ,
,取
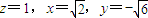 ,∴
,∴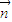 =(
=(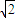 ,-
,-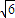 ,1),
,1),又
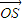 =(0,0,2
=(0,0,2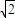 )为平面ABC的一个法向量,
)为平面ABC的一个法向量,∴
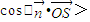 =
=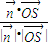 =
= .
.由图知
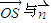 的夹角即为二面角N-CM-B的大小,其余弦值为
的夹角即为二面角N-CM-B的大小,其余弦值为 .
.(3)由(2)得
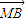 =(-1,
=(-1,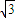 ,0),
,0),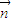 =(
=(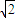 ,-
,-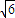 ,1)为平面CMN的一个法向量,
,1)为平面CMN的一个法向量,∴点B到平面CMN的距离即为
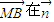 上射影的绝对值
上射影的绝对值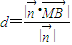 =
=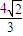 .
.点评:本题考查证明面面垂直的方法,求二面角的大小,点到平面的距离,求平面的法向量的坐标是解题的关键和易错点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
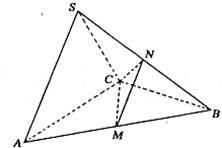 如图,三棱锥S-ABC中,△ABC是边长为4的正三角形,
如图,三棱锥S-ABC中,△ABC是边长为4的正三角形, 如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为
如图正三棱锥S-ABC的侧棱与底面边长相等,如果E、F分别是SC、AB的中点,那么异面直线EF与SA所成的角为

 ,SC=AC=BC=
,SC=AC=BC= ,M为SB中点,N在AB上,满足MN 丄 BC.
,M为SB中点,N在AB上,满足MN 丄 BC.