题目内容
在三棱锥V-ABC中，若VA=VC，AB=BC，则VB，AC所在直线的位置关系是（ ）
分析：取AC的中点O，连接VO，BO，证明AC⊥平面VOB，即可证得结论．
解答：
解：取AC的中点O，连接VO，BO
∵VA=VC，AB=BC，
∴AC⊥VO，AC⊥BO
∵VO∩BO=O
∴AC⊥平面VOB
∵VB?平面VOB
∴AC⊥VB
故选C．
解：取AC的中点O，连接VO，BO∵VA=VC，AB=BC，
∴AC⊥VO，AC⊥BO
∵VO∩BO=O
∴AC⊥平面VOB
∵VB?平面VOB
∴AC⊥VB
故选C．
点评：本题考查线面垂直，考查线线垂直，解题的关键是证明线面垂直，属于基础题．
练习册系列答案
相关题目
如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D是AB的中点，且AC=BC=a，∠VDC=θ（0＜θ＜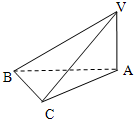
如图，在三棱锥V-ABC中，VA⊥平面ABC，∠ABC=90°，且AC=2BC=2VA=4．
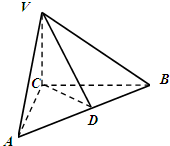如图，在三棱锥V-ABC中，VC⊥底面ABC，AC⊥BC，D是AB的中点，且AC=BC=2，
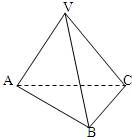（2012•增城市模拟）如图，在三棱锥V-ABC中，