题目内容
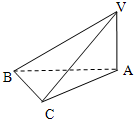 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.(1)求证:平面VBA⊥平面VBC;
(2)求:VV-ABC.
分析:(1)依题意,可证BC⊥平面VBA,从而可得平面VBA⊥平面VBC;
(2)由(1)知BC⊥平面VBA,由题意可求得AB=2
,BC=2,VA=2,从而可求得VV-ABC.
(2)由(1)知BC⊥平面VBA,由题意可求得AB=2
| 3 |
解答:证明:(1)∵VA⊥平面ABC,
∴VA⊥BC,(2分)
又∠ABC=90°,
∴BC⊥AB,(3分)
∴BC⊥平面VBA(5分)
∴平面VBA⊥平面VBC;(7分)
(2)∵∠ABC=90°,AC=2BC=2VA=4,
∴VA=VB=2(8分)
∴AB=2
,BC=2,VA=2(10分)
∴VV-ABC=
×
AB•BC•VA
=
×2
×2×2
=
(14分)

∴VA⊥BC,(2分)
又∠ABC=90°,
∴BC⊥AB,(3分)
∴BC⊥平面VBA(5分)
∴平面VBA⊥平面VBC;(7分)
(2)∵∠ABC=90°,AC=2BC=2VA=4,
∴VA=VB=2(8分)
∴AB=2
| 3 |
∴VV-ABC=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 6 |
| 3 |
=
4
| ||
| 3 |
点评:本题考查平面与平面垂直的判定,考查棱柱的体积公式,证得BC⊥平面VBA是关键,属于中档题.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.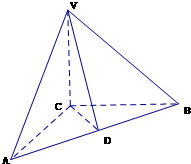 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.