Question

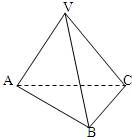（2012•增城市模拟）如图，在三棱锥V-ABC中，AB=2

3

VC=1，VA=VB=AC=BC=2．
（1）求证：AB⊥VC；
（2）求V_V-ABC．

Answer 1

分析：（1）证明AB⊥VC，只需证明AB⊥平面CDV，取AB的中点D，连VD，CD（，利用VA=VB，AC=BC，即可证得；
（2）利用V_V-ABC=V_A-VCD+V_B-VCD，即可求得结论．

解答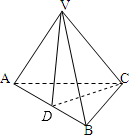：（1）证明：取AB的中点D，连VD，CD（1分）
∵VA=VB，AC=BC，∴VD⊥AB，CD⊥AB（3分）
∵VD∩CD=D
∴AB⊥平面CDV（5分）
∵VC?平面CDV
∴AB⊥VC（7分）
（2）解：∵VA=VB=AC=BC=2，AB=2

3

，
∴VD=CD=

VA2-AD2

=1（9分）
∵VC=1，∴S△VCD=

3

4

（10分）
∵AB⊥平面CDV
∴V_V-ABC=V_A-VCD+V_B-VCD（11分）=

1

3

•S△VCD•AB（13分）
=

1

3

•

3

4

•2

3

=

1

2

（14分）

点评：本题考查线面垂直，考查三棱锥的体积，解题的关键是掌握线面垂直的判定定理，正确运用三棱锥的体积公式．