题目内容
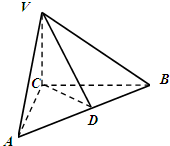 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=2,VC=
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=2,VC=| 2 |
(1)求证:平面VAB⊥平面VCD;
(2)求二面角V-AB-C的大小;
(3)求点C到平面VAB的距离.
分析:(1)三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,以CA为x轴,以CB为y轴,以CV为z轴,建立空间直角坐标系,由此能够证明AB⊥平面VCD,故平面VAB⊥平面VCD.
(2)由AB⊥平面VCD,知∠VDC是二面角V-AB-C的平面角,由此能求出二面角V-AB-C的大小.
(3)先求出平面VAB的法向量
=(1,1,
),利用向量法能够求出点C到平面VAB的距离.
(2)由AB⊥平面VCD,知∠VDC是二面角V-AB-C的平面角,由此能求出二面角V-AB-C的大小.
(3)先求出平面VAB的法向量
| n |
| 2 |
解答: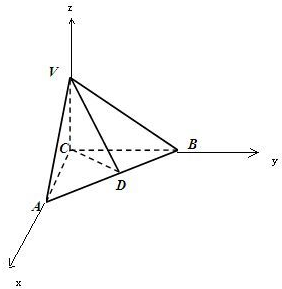 (1)证明:∵三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,
(1)证明:∵三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,
∴以CA为x轴,以CB为y轴,以CV为z轴,建立空间直角坐标系,
∵D是AB的中点,且AC=BC=2,VC=
,
∴V(0,0,
),A(2,0,0),B(0,2,0),D(1,1,0),C(0,0,0)
∴
=(1,1,0),
=(-2,2,0),
=(0,0,
),
∴
•
=-2+2+0=0,
•
=0+0+0=0,
故AB⊥CD,AB⊥CV,
∴AB⊥平面VCD,
∵AB?平面VAB,
∴平面VAB⊥平面VCD.
(2)解:由(1)知AB⊥平面VCD,
∴∠VDC是二面角V-AB-C的平面角,
∵AC=BC=2,VC=
,VC⊥底面ABC,AC⊥BC,
∴VC=CD=
,VC⊥CD,
∴∠VDC=
,
故二面角V-AB-C的大小为
.
(3)解:∵V(0,0,
),A(2,0,0),B(0,2,0),C(0,0,0),
∴
=(2,0,-
),
=(0,2,-
),
=(0,0,
),
设平面VAB的法向量为
=(x,y,z),
则
•
=0,
•
=0,
∴
,解得
=(1,1,
),
∴点C到平面VAB的距离d=
=
=1.
 (1)证明:∵三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,
(1)证明:∵三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,∴以CA为x轴,以CB为y轴,以CV为z轴,建立空间直角坐标系,
∵D是AB的中点,且AC=BC=2,VC=
| 2 |
∴V(0,0,
| 2 |
∴
| CD |
| AB |
| CV |
| 2 |
∴
| AB |
| CD |
| AB |
| CV |
故AB⊥CD,AB⊥CV,
∴AB⊥平面VCD,
∵AB?平面VAB,
∴平面VAB⊥平面VCD.
(2)解:由(1)知AB⊥平面VCD,
∴∠VDC是二面角V-AB-C的平面角,
∵AC=BC=2,VC=
| 2 |
∴VC=CD=
| 2 |
∴∠VDC=
| π |
| 4 |
故二面角V-AB-C的大小为
| π |
| 4 |
(3)解:∵V(0,0,
| 2 |
∴
| VA |
| 2 |
| VB |
| 2 |
| CV |
| 2 |
设平面VAB的法向量为
| n |
则
| n |
| VA |
| n |
| VB |
∴
|
| n |
| 2 |
∴点C到平面VAB的距离d=
|
| ||||
|
|
| |0+0+2| |
| 2 |
点评:本题考查平面垂直的证明,考查二面角大小的求法,考查点到平面的距离的求法.解题时要认真审题,注意等价转化思想和向量法的合理运用.

练习册系列答案
 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案
相关题目
 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ<
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ(0<θ< 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=θ 如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.
如图,在三棱锥V-ABC中,VA⊥平面ABC,∠ABC=90°,且AC=2BC=2VA=4.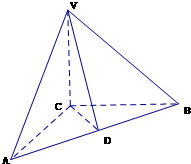 如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°.
如图,在三棱锥V-ABC中,VC⊥底面ABC,AC⊥BC,D是AB的中点,且AC=BC=a,∠VDC=45°. .
.