题目内容
2.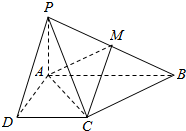 已知四棱锥P-ABCD的底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.
已知四棱锥P-ABCD的底面ABCD为直角梯形,AB∥CD,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=$\frac{1}{2}$AB=1,M是PB的中点.(1)求异面直线AC与PB所成的角的余弦值;
(2)求直线BC与平面ACM所成角的正弦值.
分析 (1)建立空间直角坐标系,利用空间向量的数量积,求AC与PB所成的角的余弦值,
(2)设$\overrightarrow{n}$=(x,y,z)为平面的ACM的一个法向量,求出法向量,利用空间向量的数量积,直线BC与平面ACM所成角的正弦值.
解答 解:(1)以A为坐标原点,分别以AD、AB、AP为x、y、z轴,建立空间直角坐标系,
则A(0,0,0),P(0,0,1),C(1,1,0),B(0,2,0),M(0,1,$\frac{1}{2}$),
所以$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{PB}$=(0,2,-1),|$\overrightarrow{AC}$|=$\sqrt{2}$,|$\overrightarrow{PB}$|=$\sqrt{5}$,
$\overrightarrow{AC}•\overrightarrow{PB}$=2,
cos($\overrightarrow{AC}$,$\overrightarrow{PB}$)=$\frac{\overrightarrow{AC}•\overrightarrow{PB}}{|\overrightarrow{AC}||\overrightarrow{PB}|}$=$\frac{\sqrt{10}}{5}$,
(2)$\overrightarrow{BC}$=(1,-1,0),$\overrightarrow{AC}$=(1,1,0),$\overrightarrow{AM}$=(0,1,$\frac{1}{2}$),
设$\overrightarrow{n}$=(x,y,z)为平面的ACM的一个法向量,则$\left\{\begin{array}{l}{\overrightarrow{AC}•\overrightarrow{n}=0}\\{\overrightarrow{AM}•\overrightarrow{n}=0}\end{array}\right.$,即$\left\{\begin{array}{l}{x+y=0}\\{y+\frac{1}{2}z=0}\end{array}\right.$,
令x=1,则y=-1,z=2,
所以$\overrightarrow{n}$=(1,-1,2),
则cos<$\overrightarrow{n}$,$\overrightarrow{BC}$>=$\frac{\overline{n}•\overrightarrow{BC}}{|\overrightarrow{n}||\overrightarrow{BC}|}$=$\frac{1+1}{\sqrt{2}×\sqrt{6}}$=$\frac{\sqrt{3}}{3}$,
设直线BC与平面ACM所成的角为α,
则sinα=sin[$\frac{π}{2}$-<$\overrightarrow{n}$,$\overrightarrow{BC}$>]=cos<$\overrightarrow{n}$,$\overrightarrow{BC}$>=$\frac{\sqrt{3}}{3}$.
点评 本小题考查空间中的异面直线所成的角、线面角、解三角形等基础知识考查空间想象能力和思维能力.

 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案| A. | $\frac{1}{5}$ | B. | $-\frac{1}{5}$ | C. | $\frac{1}{7}$ | D. | $-\frac{1}{7}$ |
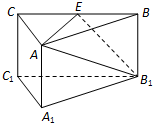 如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )
如图,三棱柱A1B1C1-ABC中,侧棱AA1⊥底面A1B1C1,底面三角形A1B1C1是正三角形,E是BC中点,则下列叙述正确的是( )| A. | CC1与B1E是异面直线 | B. | AC⊥平面ABB1A1 | ||
| C. | A1C1∥平面AB1E | D. | AE,B1C1为异面直线,且AE⊥B1C1 |
| A. | 45° | B. | 60° | C. | 90° | D. | 120° |