题目内容
17．若实数x，y满足约束条件$\left\{\begin{array}{l}y≤2-x\\ x-y≤2\\ 2x-y+2≥0\end{array}\right.$，则z=x-2y的最小值为-4．分析 作$\left\{\begin{array}{l}y≤2-x\\ x-y≤2\\ 2x-y+2≥0\end{array}\right.$表示的平面区域，化简目标函数z=x-2y为y=$\frac{1}{2}x$-$\frac{z}{2}$，从而解得．
解答 解：作$\left\{\begin{array}{l}y≤2-x\\ x-y≤2\\ 2x-y+2≥0\end{array}\right.$表示的平面区域如下，
z=x-2y可化为y=$\frac{1}{2}x$-$\frac{z}{2}$，
故当过点（0，2）时，-$\frac{z}{2}$有最大值，z=x-2y有最小值-4；
故答案为：-4．
点评 本题考查了线性规划的应用及数形结合的思想应用．
练习册系列答案
海淀黄冈名师导航系列答案
普通高中同步练习册系列答案
相关题目
8．数列-1，3，-7，15，…的通项公式an等于（ ）
| A． | （-1）n+1（2n-1） | B． | （-1）n2n+1 | C． | （-1）n（2n-1） | D． | 2n-1 |
5．计算$cos\frac{π}{3}$-$tan\frac{π}{4}$+$\frac{3}{4}ta{n^2}\frac{π}{6}$-$sin\frac{π}{6}$+$co{s^2}\frac{π}{6}$的结果为（ ）
| A． | -$\frac{1}{2}$ | B． | $\frac{{\sqrt{3}-1}}{2}$ | C． | 0 | D． | $\frac{{\sqrt{3}}}{2}$ |
12．下列函数中，既是偶函数又在（-∞，0）上单调递增的是（ ）
| A． | y=x2 | B． | y=2|x| | C． | y=sin x | D． | y=log2$\frac{1}{|x|}$ |
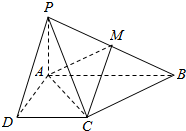已知四棱锥P-ABCD的底面ABCD为直角梯形，AB∥CD，∠DAB=90°，PA⊥底面ABCD，且PA=AD=DC=$\frac{1}{2}$AB=1，M是PB的中点．