题目内容
(本小题满分14分)
一个几何体的三视图如右图所示,其中正视图和侧视图是腰长为6的两个全等的等腰直角三角形.
(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值。

(Ⅰ)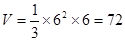 ;
;
(Ⅱ)依题意,正方体的体积是原四棱锥体积的3倍,故用3个这样的四棱锥可以拼成一个棱长为6的正方体, 证明:见解析;
(Ⅲ)平面AB1E与平面ABC所成二面角的余弦值为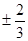 .
.
【解析】本试题主要是考查了三视图和空间几何体的体积公式的运用,以及求解二面角的平面角的综合运用。
(1)由于三视图风影的几何体是四棱锥,一条侧棱垂直底面,画出图形,根据三视图的数据,求出四棱锥的体积.
(2)依题意,正方体的体积是原四棱锥体积的3倍,
故用3个这样的四棱锥可以拼成一个棱长为6的正方体,
(3)设B1E,BC的延长线交于点G,
连结GA,在底面ABC内作BH⊥AG,垂足为H,
连结HB1,则B1H⊥AG,故∠B1HB为平面AB1E与
平面ABC所成二面角或其补角的平面角,然后借助于三角形得到求解。
解:(Ⅰ)该几何体的直观图如图1所示,它是有一条侧棱垂直于底面的四棱锥. 其中底面ABCD是边长为6的正方形,高为CC1=6,故所求体积是
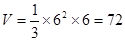 ------------------------4分
------------------------4分
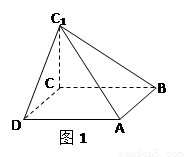
(Ⅱ)依题意,正方体的体积是原四棱锥体积的3倍,
故用3个这样的四棱锥可以拼成一个棱长为6的正方体,
其拼法如图2所示. ------------------------6分
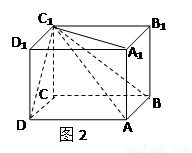
证明:∵面ABCD、面ABB1A1、面AA1D1D为全等的
正方形,于是
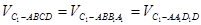 故所拼图形成立.---8分
故所拼图形成立.---8分
(Ⅲ)方法一:设B1E,BC的延长线交于点G,
连结GA,在底面ABC内作BH⊥AG,垂足为H,
连结HB1,则B1H⊥AG,故∠B1HB为平面AB1E与
平面ABC所成二面角或其补角的平面角. --------10分
在Rt△ABG中,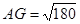 ,则
,则
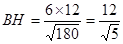 ,
,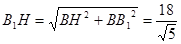 ,
,
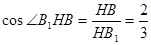 ,故平面AB1E与平面ABC所成二面角的余弦值为
,故平面AB1E与平面ABC所成二面角的余弦值为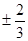 .---14分
.---14分
方法二:以C为原点,CD、CB、CC1所在直线分别为x、y、z轴建立直角坐标系(如图3),

∵正方体棱长为6,则E(0,0,3),B1(0,6,6),A(6,6,0).
设向量n=(x,y,z),满足n⊥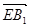 ,n⊥
,n⊥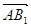 ,
,
于是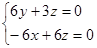 ,解得
,解得 .
--------------------12分
.
--------------------12分
取z=2,得n=(2,-1,2). 又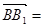 (0,0,6),
(0,0,6),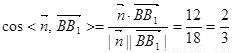 故平面AB1E与平面ABC所成二面角的余弦值为
故平面AB1E与平面ABC所成二面角的余弦值为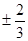 . -------------14分
. -------------14分

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)