题目内容
(本小题满分14分)设椭圆C1的方程为![]() (a>b>0),曲线C2的方程为y=
(a>b>0),曲线C2的方程为y=![]() ,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
,且曲线C1与C2在第一象限内只有一个公共点P。(1)试用a表示点P的坐标;(2)设A、B是椭圆C1的两个焦点,当a变化时,求△ABP的面积函数S(a)的值域;(3)记min{y1,y2,……,yn}为y1,y2,……,yn中最小的一个。设g(a)是以椭圆C1的半焦距为边长的正方形的面积,试求函数f(a)=min{g(a), S(a)}的表达式。
(Ⅰ) (![]() ). (Ⅱ) S(a)的值域为(0,
). (Ⅱ) S(a)的值域为(0,![]() ) (Ⅲ)S(a)}
) (Ⅲ)S(a)}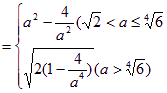
解析:
(1)将y=![]() 代入椭圆方程,得
代入椭圆方程,得![]() 化简,得b2x4–a2b2x2+a2=0
化简,得b2x4–a2b2x2+a2=0
由条件,有Δ=a4b4–4a2b2=0,得ab=2解得x=![]() 或x=–
或x=–![]() (舍去)
(舍去)
故P的坐标为(![]() ).
).
(2)∵在△ABP中,|AB|=2![]() ,高为
,高为![]() ,∴
,∴![]()
∵a>b>0,b=![]() ∴a>
∴a>![]() ,即a>
,即a>![]() ,得0<
,得0<![]() <1
<1
于是0<S(a)<![]() ,故△ABP的面积函数S(a)的值域为(0,
,故△ABP的面积函数S(a)的值域为(0,![]() )
)
(3)g(a)=c2=a2–b2=a2–![]() 解不等式g(a)≥S(a),即a2–
解不等式g(a)≥S(a),即a2–![]() ≥
≥![]()
整理,得a8–10a4+24≥0,即(a4–4)(a4–6)≥0
解得a≤![]() (舍去)或a≥
(舍去)或a≥![]() .故f(a)=min{g(a), S(a)}
.故f(a)=min{g(a), S(a)}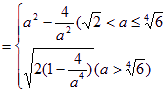

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)