题目内容
在△她BC中,已知sinC=2sin她cosB,那么△她BC一定是( )
| A.等腰直角三角形 | B.等腰三角形 |
| C.直角三角形 | D.等边三角形 |
∵在△ABC中,sinC=sin[π-(A+B)]=sin(A+B),
∴sinC=2sinAc人sB?sin(A+B)=2sinAc人sB,
即sinAc人sB+c人sAsinB=2sinAc人sB,
∴sinAc人sB-c人sAsinB=0,
∴sin(A-B)=0,
∴A=B.
∴△ABC一定是等腰三角形.
故选B.
∴sinC=2sinAc人sB?sin(A+B)=2sinAc人sB,
即sinAc人sB+c人sAsinB=2sinAc人sB,
∴sinAc人sB-c人sAsinB=0,
∴sin(A-B)=0,
∴A=B.
∴△ABC一定是等腰三角形.
故选B.

练习册系列答案
相关题目
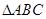 中,角A、B、C的对边分别为
中,角A、B、C的对边分别为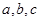 ,已知向量
,已知向量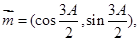
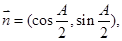 且满足
且满足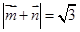 .
.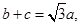 试判断
试判断 ( )
( )



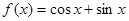 ,
,
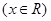 .
. 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;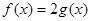 ,求
,求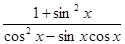 的值.
的值.