题目内容
16.已知公差大于零的等差数列{an},各项均为正数的等比数列{bn},满足a1=1,b1=2,a4=b2,a8=b3.(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)若数列{cn}满足cn=$\left\{\begin{array}{l}{a_n},n为偶数\\{b_n},n为奇数\end{array}$,求数列{cn}的前2n项和T2n.
分析 (I)设等差数列{an}的公差为d>0,各项均为正数的等比数列{bn}的公比为q,利用等差数列与等比数列的通项公式即可得出;
(II)由于偶数项是公差为2等差数列,奇数项是公比为4等比数列,因此对数列{cn}的前2n项和T2n分组求和可得:T2n=(2+23+…+22n-1)+(2+4+…+2n),
再利用等差数列与等比数列的前n项和公式即可得出.
解答 解:(I)设等差数列{an}的公差为d>0,各项均为正数的等比数列{bn}的公比为q,
∵a1=1,b1=2,a4=b2,a8=b3.
∴$\left\{\begin{array}{l}{1+3d=2q}\\{1+7d=2{q}^{2}}\end{array}\right.$,解得$\left\{\begin{array}{l}{d=1}\\{q=2}\end{array}\right.$.
∴an=1+(n-1)=n,bn=2n.
(II)由于偶数项是公差为2等差数列,奇数项是公比为4等比数列,因此对数列{cn}的前2n项和T2n分组求和可得:
T2n=(2+23+…+22n-1)+(2+4+…+2n)
=$\frac{2({4}^{n}-1)}{4-1}$+$\frac{n(2+2n)}{2}$
=$\frac{2}{3}({4}^{n}-1)$+n(n+1).
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式、“分组求和”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
7.已知集合M={1,2},N={x|log2(2x-1)≤2},则M∩N( )
| A. | {1} | B. | {2} | C. | {0,1} | D. | {1,2} |
1.已知复数z=$\frac{\sqrt{3}-i}{1+\sqrt{3}i}$,则|z|=( )
| A. | 1 | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{16}$ |
8.在等差数列{an}中,a3=4,d=2,则a7=( )
| A. | 12 | B. | 13 | C. | 11 | D. | 14 |
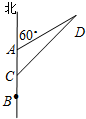 如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.
如图,机车甲、乙分别停在A,B处,且AB=10km,甲的速度为4千米/小时,乙的速度是甲的$\frac{1}{2}$,甲沿北偏东60°的方向移动,乙沿正北方向移动,若两者同时移动100分钟,则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米.