题目内容
11．
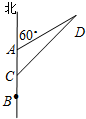如图，机车甲、乙分别停在A，B处，且AB=10km，甲的速度为4千米/小时，乙的速度是甲的$\frac{1}{2}$，甲沿北偏东60°的方向移动，乙沿正北方向移动，若两者同时移动100分钟，则它们之间的距离为$\frac{20\sqrt{3}}{3}$千米．
分析 由原题求出AD，BC，利用余弦定理求解即可．
解答 解：甲的速度为4千米/小时，移动100分钟，可得AD=$\frac{4}{60}×100=\frac{20}{3}$千米．
甲的速度为4千米/小时，乙的速度是甲的$\frac{1}{2}$，乙沿正北方向移动，移动100分钟，
可得BC=$\frac{1}{2}×\frac{4}{60}×100=\frac{10}{3}$千米，AC=10-$\frac{10}{3}$=$\frac{20}{3}$千米．
∠DAC=120°，
CD=$\sqrt{{AC}^{2}+{AD}^{2}-2AD•ACcos120°}$=$\frac{20\sqrt{3}}{3}$．（千米）．
故答案为：$\frac{{20\sqrt{3}}}{3}$．
点评 本题考查三角形的解法，余弦定理的应用，考查计算能力．
练习册系列答案
相关题目
6．若实数x，y满足约束条件$\left\{\begin{array}{l}x+y≤4\\ x-2y-4≤0\\ x≥1\end{array}\right.$，则点P（x，y）落在圆（x-1）2+（y-3）2=4内的概率为（ ）
| A． | $\frac{π}{27}$ | B． | $\frac{2π}{27}$ | C． | $\frac{π}{9}$ | D． | $\frac{2π}{9}$ |