题目内容
已知 ,
, ,其中
,其中 ,若函数
,若函数 ,且函数
,且函数 的图象与直线y=2两相邻公共点间的距离为
的图象与直线y=2两相邻公共点间的距离为 .
.
(l)求 的值;
的值;
(2)在△ABC中,以a,b,c(分别是角A,B,C的对边,且 ,求△ABC周长的取值范围.
,求△ABC周长的取值范围.
(1)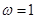 ;(2)
;(2) .
.
解析试题分析:(1)先根据 ,结合二倍角公式以及和角公式化简,求得
,结合二倍角公式以及和角公式化简,求得 ,函数最大值是
,函数最大值是 ,那么函数
,那么函数 的图像与直线
的图像与直线 两相邻公共点间的距离
两相邻公共点间的距离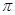 正好是一个周期,然后根据
正好是一个周期,然后根据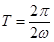 求解
求解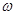 的值;(2)先将
的值;(2)先将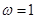 代入函数
代入函数 的解析式得到:
的解析式得到: ,由已知条件
,由已知条件 以及
以及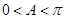 ,结合三角函数的图像与性质可以解得
,结合三角函数的图像与性质可以解得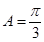 ,所以
,所以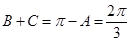 ,由正弦定理得
,由正弦定理得 ,那么
,那么 的周长可以表示为:
的周长可以表示为: ,由差角公式以及和角公式将此式化简整理得,
,由差角公式以及和角公式将此式化简整理得,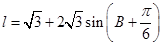 ,结合角
,结合角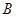 的取值以及三角函数的图像与性质可得
的取值以及三角函数的图像与性质可得 .
.
试题解析:(1)
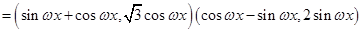


 , 3分
, 3分
∵ ,
,
∴函数 的周期
的周期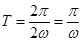 ,
,
∵函数 的图象与直线
的图象与直线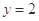 两相邻公共点间的距离为
两相邻公共点间的距离为 .
.
∴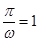 ,解得
,解得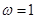 . 4分
. 4分
(2)由(Ⅰ)可知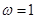 ,
, ,
,
∵ ,∴
,∴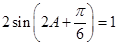 ,即
,即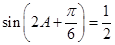 ,
,
又∵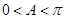 ,∴
,∴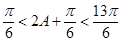 ,
,
∴ ,解得
,解得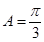 . 7分
. 7分
由正弦定理得: ,
,
所以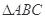 周长为:
周长为: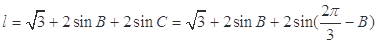
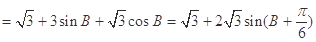 , 10分
, 10分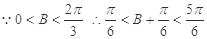 ,
,
所以三角形周长的取值范围是 . 12分
. 12分
考点:1.和角公式;2.差角公式;3.二倍角公式;4.三角函数的图像与性质;5.正弦定理

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 ,
, .
. 为何值时,
为何值时, 取得最大值,并求出其最大值;
取得最大值,并求出其最大值; ,
, ,求
,求 的值.
的值. 的图象(部分)如图所示.
的图象(部分)如图所示.
 的解析式;
的解析式; ,求函数
,求函数 =(2cos
=(2cos ,1),
,1), =(cos
=(cos sin2
sin2 =
= R.
R. [
[ ,
, ],求
],求 =
= (
( )与
)与 ,2),求函数
,2),求函数
 ,设函数
,设函数
 的图象关于直线
的图象关于直线 对称,其中常数
对称,其中常数

 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图像,用五点法作出函数
的图像,用五点法作出函数 的图像.
的图像.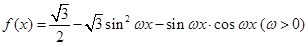 ,且
,且 图象的相邻两条对称轴间的距离为
图象的相邻两条对称轴间的距离为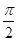 ,
,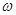 的值;
的值;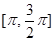 上的值域.
上的值域. <C<
<C< ,且
,且 =
= .
. +
+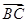 |=2,求
|=2,求 在一个周期内的图象如图所示,点
在一个周期内的图象如图所示,点 为图象的最高点,
为图象的最高点, 为图象与
为图象与 轴的交点,且三角形
轴的交点,且三角形 的面积为
的面积为 .
.
 的值及函数
的值及函数 的值域;
的值域; ,求
,求 的值.
的值. (其中
(其中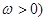 的最小正周期为
的最小正周期为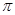 .
. 的值,并求函数
的值,并求函数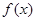 的单调递减区间;
的单调递减区间;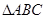 中,
中, 分别是角
分别是角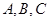 的对边,若
的对边,若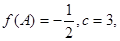
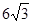 ,求
,求