题目内容
已知椭圆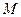 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线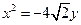 的焦点是椭圆
的焦点是椭圆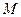 的一个焦点,又点
的一个焦点,又点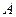
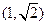 在椭圆
在椭圆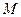 上.
上.
(Ⅰ)求椭圆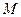 的方程;
的方程;
(Ⅱ)已知直线 的方向向量为
的方向向量为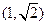 ,若直线
,若直线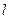 与椭圆
与椭圆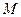 交于
交于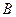 、
、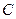 两点,求
两点,求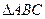 面积的最大值.
面积的最大值.
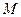 的对称轴为坐标轴,且抛物线
的对称轴为坐标轴,且抛物线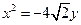 的焦点是椭圆
的焦点是椭圆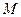 的一个焦点,又点
的一个焦点,又点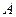
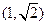 在椭圆
在椭圆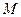 上.
上.(Ⅰ)求椭圆
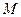 的方程;
的方程;(Ⅱ)已知直线
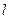 的方向向量为
的方向向量为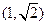 ,若直线
,若直线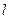 与椭圆
与椭圆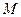 交于
交于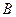 、
、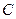 两点,求
两点,求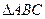 面积的最大值.
面积的最大值.解: (Ⅰ)由已知抛物线的焦点为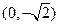 ,故设椭圆方程为
,故设椭圆方程为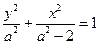 .
.
将点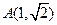 代入方程得
代入方程得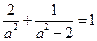 ,整理得
,整理得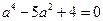 ,
,
解得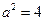 或
或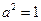 (舍).
(舍).
故所求椭圆方程为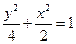 . -------------------(6分)
. -------------------(6分)
(Ⅱ)设直线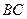 的方程为
的方程为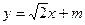 ,设
,设
代入椭圆方程并化简得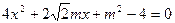 ,
,
由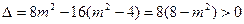 ,可得
,可得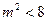 . (
. ( 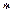 )
)
由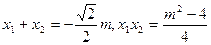 ,
,
故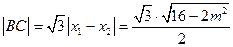 .
.
又点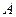 到
到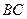 的距离为
的距离为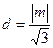 ,
,
故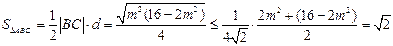 ,
,
当且仅当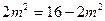 ,即
,即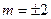 时取等号(满足
时取等号(满足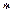 式)
式)
所以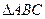 面积的最大值为
面积的最大值为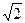 . ----------------(12分)
. ----------------(12分)
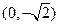 ,故设椭圆方程为
,故设椭圆方程为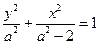 .
.将点
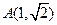 代入方程得
代入方程得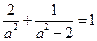 ,整理得
,整理得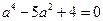 ,
,解得
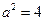 或
或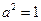 (舍).
(舍).故所求椭圆方程为
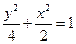 . -------------------(6分)
. -------------------(6分)(Ⅱ)设直线
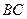 的方程为
的方程为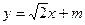 ,设
,设
代入椭圆方程并化简得
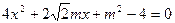 ,
, 由
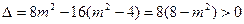 ,可得
,可得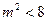 . (
. ( 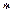 )
)由
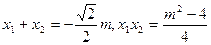 ,
,故
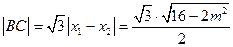 .
. 又点
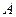 到
到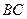 的距离为
的距离为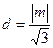 ,
, 故
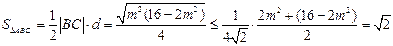 ,
,当且仅当
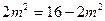 ,即
,即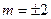 时取等号(满足
时取等号(满足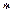 式)
式)所以
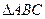 面积的最大值为
面积的最大值为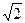 . ----------------(12分)
. ----------------(12分) 略

练习册系列答案
 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
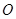 为原点,从椭圆 + =1的左焦点
为原点,从椭圆 + =1的左焦点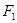 引圆
引圆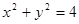 的切线
的切线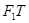 交椭圆于点
交椭圆于点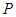 ,切点
,切点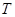 位于
位于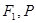 之间,
之间,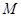 为线段
为线段 的中点,则
的中点,则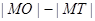 的值为_______________。
的值为_______________。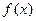 定义在区间[a, b]上,设“
定义在区间[a, b]上,设“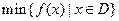 ”表示函数
”表示函数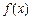 在集合D上的最小值,“
在集合D上的最小值,“ ”表示函数
”表示函数 ,
,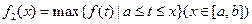 ,
,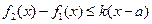 对任意的
对任意的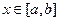 成立,则称函数
成立,则称函数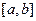 上的“第k类压缩函数”.
上的“第k类压缩函数”.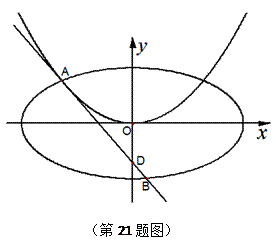
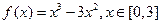 ,求
,求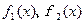 的解析式;
的解析式;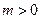 ,函数
,函数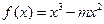 是
是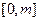 上的“第3类压缩函数”,求m的取值范围.
上的“第3类压缩函数”,求m的取值范围.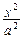 +
+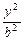 =1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数
=1(a>b>0)右焦点F且斜率为1的直线交椭圆C于A,B两点,N为弦AB的中点;又函数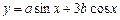 图象的一条对称轴的方程是
图象的一条对称轴的方程是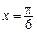 .
. C
C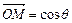
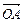 +
+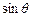
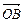 成立.
成立.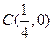 ,椭圆
,椭圆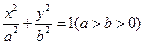 的右准线
的右准线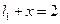 与x轴相交于点D,右焦点F到上顶点的距离为
与x轴相交于点D,右焦点F到上顶点的距离为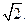
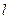 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得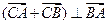 ?若存在,求出直线
?若存在,求出直线 为正数,
为正数, ,
, 其中
其中 是常数,且
是常数,且 的最小值是
的最小值是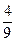 ,满足条件的点
,满足条件的点 是椭圆
是椭圆 一弦的中点,则此弦所在的直线方程为
一弦的中点,则此弦所在的直线方程为



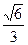

 在椭圆
在椭圆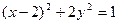 上,则
上,则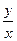 的最大值是( )
的最大值是( )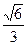
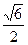
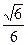
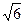
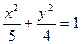 的短轴长是( )
的短轴长是( )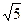

 4
4