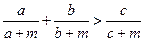题目内容
设A={x|x2-2x-3>0},B={x|x2+ax+b≤0},若A∪B=R,A∩B=(3,4],则a+b等于
| A.7 | B.-1 |
| C.1 | D.-7 |
D
A=(-∞,-1)∪(3,+∞),
∵A∪B=R,A∩B=(3,4],则B=[-1,4].
∴a=-(-1+4)=-3,b=-1×4=-4.
∵A∪B=R,A∩B=(3,4],则B=[-1,4].
∴a=-(-1+4)=-3,b=-1×4=-4.

练习册系列答案
相关题目
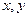 满足
满足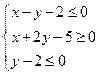 ,则
,则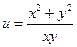 的取值范围是 ( )
的取值范围是 ( )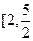 ]
]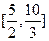
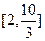
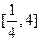
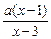 >1(a>0).
>1(a>0).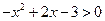 的解集.
的解集.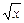 >mx+
>mx+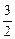 的解集为4<x<n,则m、n的值分别是
的解集为4<x<n,则m、n的值分别是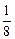 ,n="36"
,n="36"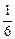 ,n=32
,n=32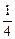 ,n="28"
,n="28"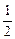 ,n=24
,n=24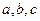 ,且
,且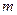 为正数,
为正数,