题目内容
15.已知椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A1,A2,且|A1A2|=4$\sqrt{3}$,该椭圆的离心率为$\frac{{\sqrt{6}}}{3}$,以M(-3,2)为圆心,r为半径的圆与椭圆C交于A,B两点.(1)求椭圆C的方程;
(2)若A,B两点关于原点对称,求圆M的方程;
(3)若点A的坐标为(0,2),求△ABM的面积.
分析 (1)由题意求出a=2$\sqrt{3}$,结合椭圆离心率求得c,再由隐含条件求得b,则椭圆C的方程可求;
(2)由A,B两点关于原点对称,可知O是AB的中点,结合垂径定理可知MO⊥AB,进一步得到直线MO的斜率,得到直线AB的斜率,则直线AB的方程可求,联立直线方程和椭圆方程,求出A的坐标由勾股定理得圆的半径,则圆M的方程可求;
(3)由题意知直线AB的斜率存在,设直线AB的方程为y=kx+2,联立直线方程和椭圆方程,化为关于x的一元二次方程,求得B的坐标,进一步得线段AB的中点E的坐标,求得直线ME的斜率,结合题意列式求得AB的斜率,得到直线AB的方程为y=x+2,求出|AB|,由点到直线的距离公式求得点M到直线AB的距离,代入△ABM的面积公式得答案.
解答 解:(1)由题意可知2a=4$\sqrt{3}$,即a=2$\sqrt{3}$,又$e=\frac{c}{a}=\frac{{\sqrt{6}}}{3}$,则$c=2\sqrt{2}$,
∴b2=${a}^{2}-{c}^{2}=(2\sqrt{3})^{2}-(2\sqrt{2})^{2}=4$,
即椭圆C的方程为$\frac{{x_{\;}^2}}{12}+\frac{{y_{\;}^2}}{4}=1$;
(2)∵A,B两点关于原点对称,∴O是AB的中点,
由垂径定理可知MO⊥AB,又M(-3,2),∴直线MO的斜率为-$\frac{2}{3}$,
故直线AB的斜率为$\frac{3}{2}$,则直线AB的方程为y=$\frac{3}{2}$x,
联立$\left\{\begin{array}{l}\frac{{x_{\;}^2}}{12}+\frac{{y_{\;}^2}}{4}=1\\ y=\frac{3}{2}x\end{array}\right.$,解得$x_A^2=\frac{48}{31},y_A^2=\frac{108}{31}$,
由勾股定理得r2=MA2=MO2+OA2=9+4+$\frac{48}{31}+\frac{108}{31}=\frac{559}{31}$,
∴圆M的方程为(x+3)2+(y-2)2=$\frac{559}{31}$;
(3)由题意知直线AB的斜率存在,设直线AB的方程为y=kx+2,
联立$\left\{\begin{array}{l}\frac{x^2}{12}+\frac{y^2}{4}=1\\ y=kx+2\end{array}\right.$,得(1+3k2)x2+12kx=0,
则B($-\frac{12k}{{1+3{k^2}}},\frac{{2-6{k^2}}}{{1+3{k^2}}}$),线段AB的中点为E($-\frac{6k}{{1+3{k^2}}},\frac{2}{{1+3{k^2}}}$),
直线ME的斜率为$\frac{{\frac{2}{{1+3{k^2}}}-2}}{{-\frac{6k}{{1+3{k^2}}}-(-3)}}=\frac{{-2{k^2}}}{{3{k^2}-2k+1}}$,
∵AB⊥ME,∴$\frac{{-2{k^2}}}{{3{k^2}-2k+1}}$•k=-1,
∴2k3-3k2+2k-1=0,即(k-1)(2k2-k+1)=0,解得k=1,
∴直线AB的方程为y=x+2,
又B(-3,-1),∴|AB|=3$\sqrt{2}$,
而点M到直线AB的距离为$\frac{{3\sqrt{2}}}{2}$,
故△ABM的面积为$\frac{1}{2}×3\sqrt{2}×\frac{{3\sqrt{2}}}{2}=\frac{9}{2}$.
点评 本题考查椭圆的简单性质,是直线与圆、圆锥曲线的综合题,训练了直线与圆锥曲线位置关系的应用,考查计算能力,属有一定难度题目.

 某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:
某车间为了规定工时定额,需要确定加工某零件所花费的时间,为此作了四次实验,得到的数据如下:| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2)求出y关于x的线性回归方程;
(3)试预测加工10个零件需要多少时间?(注:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\stackrel{∧}{y}$-$\stackrel{∧}{b}$$\overline{x}$)
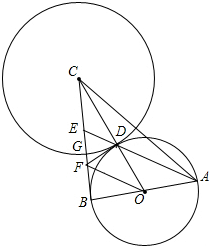 如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.
如图:Rt△ABC中,∠ABC=90°,AB=BC.以AB为直径的⊙O交OC于D,AD的延长线交BC于E,过点D作⊙O的切线DF交BC于F,连OF.⊙C切⊙O于点D,交BC于G.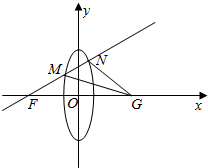 已知,椭圆C:$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0)短轴长是1,离心率e=$\frac{\sqrt{3}}{2}$.
已知,椭圆C:$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0)短轴长是1,离心率e=$\frac{\sqrt{3}}{2}$.