题目内容
下列命题错误的是
| A.命题“若m > 0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0无实数根,则m≤0”. |
| B.“x=1”是“x2-3x + 2=0”的充分不必要条件. |
C.若 为假命题,则p ,q均为假命题. 为假命题,则p ,q均为假命题. |
D.对于命题p: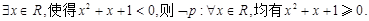 |
C
解析试题分析:四种命题的关系,主要是对于逆否命题的运用,同时利用集合的思想,能判定命题间的包含关系,从而得到充分条件的判定。
由于选项A中,若m > 0,则方程x2+x-m=0有实数根”的逆否命题为,将原命题的条件的否定作为其逆否命题的结论,将原命题中结论的否定作为其逆否命题的条件,可知为若方程x2+x-m=0无实数根,则m≤0”,因此正确。
选项B中, 命题的结论“x2-3x + 2=0”等价于x=1,或x=2,而命题的条件是x=1,可知条件表示的集合小,则利用小集合是大集合成立的充分不必要条件,故正确。
选项C,中,且命题为假命题,则说明至少有一个假命题,因此错误。
选项D中,对于特称命题的否定,就是将存在改为任意,结论变为否定即可。故正确,因此答案为C.
考点:本试题主要是考查了命题的真值,以及充分条件问题。
点评:简易逻辑的考查主要是侧重于命题的真值,以及四种命题的关系,以及充分条件的判定的考查上,属于基础题。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
①  ;②
;②  ;
;
③ 抛物线
抛物线 过原点;④
过原点;④
其中满足p是q的充要条件的命题个数为
| A.0 | B.1 | C.2 | D.3 |
下列说法正确的是( )
| A.三点确定一个平面 |
B.平面 和 和 有不同在一条直线上的三个交点 有不同在一条直线上的三个交点 |
| C.梯形一定是平面图形 |
| D.四边形一定是平面图形 |
在下列命题中,真命题是( )
| A.若“x=2,则x2-3x+2=0”的否命题; |
| B.“若b=3,则b2=9”的逆命题; |
| C.若ac>bc,则a>b; |
| D.“相似三角形的对应角相等”的逆否命题 |
已知条件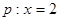 ,条件
,条件 ,则
,则 是
是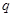 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
在原命题及其逆命题、否命题、逆否命题这四个命题中,真命题的个数可以是
| A.1个或2个或3个或4个 |
| B.0个或2个或4个 |
| C.1个或3个 |
| D.0个或4个 |
命题“对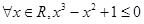 ”的否定是( )
”的否定是( )
| A.不存在x∈R,x3-x2+1≤0 | B.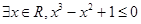 |
C. | D.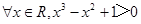 |
“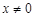 ”是“
”是“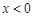 ”的 ( )
”的 ( )
| A.充分非必要条件 | B.必要非充分条件 | C.充要条件 | D.既非充分又非必要条件. |
对于实数 是
是 的( )
的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |