题目内容
下列说法正确的是( )
| A.三点确定一个平面 |
B.平面 和 和 有不同在一条直线上的三个交点 有不同在一条直线上的三个交点 |
| C.梯形一定是平面图形 |
| D.四边形一定是平面图形 |
C
解析试题分析:A.三点确定一个平面,错误,不共线的三点确定一个平面;
B.平面 和
和 有不同在一条直线上的三个交点,错误,两个平面的若有一个公共点,则有一条过该点的公共直线。
有不同在一条直线上的三个交点,错误,两个平面的若有一个公共点,则有一条过该点的公共直线。
C.梯形一定是平面图形,正确,因为两条平行直线确定一个平面,梯形的上下底边平行,所以梯形一定是平面图形;
D.四边形一定是平面图形,不正确,四边形有可能是空间四边形。
考点:平面的基本性质。
点评:我们要熟练掌握平面的基本性质,尤其是里面的关键词,更要特别注意。属于基础题型。

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目
下列说法错误的是( )
A.命题“若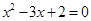 ,则 ,则 ”的逆否命题为:“若 ”的逆否命题为:“若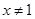 ,则 ,则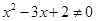 ” ” |
B.“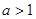 ”是“ ”是“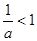 ”的充分不必要条件 ”的充分不必要条件 |
C.若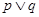 为真命题,则 为真命题,则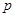 、 、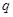 均为真命题 均为真命题 |
D.若命题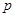 :“存在 :“存在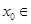 R, R,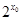 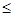 0”,则 0”,则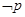 :“对任意的 :“对任意的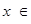 R, R,  >0”. >0”. |
已知q是等比数列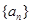 的公比,则“
的公比,则“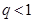 ”是“数列
”是“数列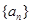 是递减数列”的( )
是递减数列”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题是真命题的是
A.若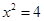 ,则 ,则 | B.若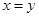 ,则 ,则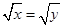 |
C.若 ,则 ,则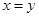 | D.若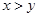 ,则 ,则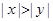 |
命题“若α= ,则tanα=1”的逆否命题是
,则tanα=1”的逆否命题是
A.若α≠ ,则tanα≠1 ,则tanα≠1 | B.若α= ,则tanα≠1 ,则tanα≠1 |
C.若tanα≠1,则α≠ | D.若tanα≠1,则α= |
已知 ,命题“若
,命题“若 ,则
,则 ”的逆否命题是( ).
”的逆否命题是( ).
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则 ,则 |
D.若 ,则 ,则 |
设 ∶
∶ ,
, ∶
∶ ,则
,则 是
是 的
的
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题错误的是
| A.命题“若m > 0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0无实数根,则m≤0”. |
| B.“x=1”是“x2-3x + 2=0”的充分不必要条件. |
C.若 为假命题,则p ,q均为假命题. 为假命题,则p ,q均为假命题. |
D.对于命题p: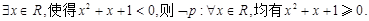 |
 中,若
中,若 ,则
,则 ;
; ,则
,则 在
在 上的投影为
上的投影为 ;
; ,
, ,则“
,则“ ”为假命题;
”为假命题;
 的导函数的最大值为
的导函数的最大值为 ,则函数
,则函数 的图
的图 对称.
对称.