题目内容
17.设函数f(x)=$\frac{{1+{{({-1})}^x}}}{2}({x∈z})$,给出以下三个结论:①f(x)为偶函数;②f(x)为周期函数;③f(x+1)+f(x)=1,其中正确结论的个数为( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 由题意可得f(x)=$\frac{1+(-1)^{x}}{2}$=$\left\{\begin{array}{l}{1,x为偶数}\\{0,x为奇数}\end{array}\right.$,检验f(-x)=f(x),即可判断①,由于f(x)的函数值是1,0交替出现,故函数是以2为周期的周期函数,可判断②,由于x+1,x中必定一个是奇数,一个是偶数,则f(x+1)与f(x)的值一个是1,一个是0,可判断③.
解答 解:∵f(x)=$\frac{1+(-1)^{x}}{2}$=$\left\{\begin{array}{l}{1,x为偶数}\\{0,x为奇数}\end{array}\right.$,
∴f(-x)=$\frac{1+(-1)^{-x}}{2}$=$\frac{1+\frac{1}{(-1)^{x}}}{2}$=$\left\{\begin{array}{l}{1,x为偶数}\\{0,x为奇数}\end{array}\right.$=f(x),故f(x)为偶函数,①正确.
由于f(x)的函数值是1,0交替出现,故函数是以2为周期的周期函数,②正确.
由于x+1,x中必定一个是奇数,一个是偶数,则f(x+1)与f(x)的值一个是1,一个是0,则f(x+1)+f(x)=1,③正确.
∴正确结论的个数为:3.
故选:D.
点评 本题主要考查了函数的奇偶性的定义、周期性的定义的应用,解题的关键是对已知函数的化简,是基础题.

练习册系列答案
相关题目
 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).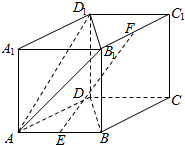 如图,在四棱柱 ABCD-A1 B1C1D1中,CC1⊥底面 ABCD,底面 ABCD为菱形,点 E,F分别是 AB,B1C1的中点,且∠DAB=60°,AA1=AB=2.
如图,在四棱柱 ABCD-A1 B1C1D1中,CC1⊥底面 ABCD,底面 ABCD为菱形,点 E,F分别是 AB,B1C1的中点,且∠DAB=60°,AA1=AB=2.