题目内容
8. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点为F,A为短轴的一个端点,且|OA|=|OF|,△AOF的面积为1(其中O为坐标原点).(1)求椭圆的方程;
(2)若C,D分别是椭圆长轴的左、右端点,动点M满足MD⊥CD,连接CM,交椭圆于点P,证明:$\overrightarrow{OM}$•$\overrightarrow{OP}$为定值.
分析 (1)由题意可得b=c,$\frac{1}{2}$bc=1,解方程可得b,c,由a,b,c的关系,解得a=2,进而得到椭圆方程;
(2)设出直线MC的方程,代入椭圆方程,求得P的坐标,M的坐标,由向量的数量积的坐标表示计算即可得到定值4.
解答  解:(1)由题意可得b=c,$\frac{1}{2}$bc=1,
解:(1)由题意可得b=c,$\frac{1}{2}$bc=1,
解得b=c=$\sqrt{2}$,a=$\sqrt{{b}^{2}+{c}^{2}}$=2,
即有椭圆的方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1;
(2)由题意直线MC的斜率存在,
设其方程为y=k(x+2),
代入椭圆方程x2+2y2=4,得
(1+2k2)x2+8k2x+8k2-4=0,
由xP(-2)=$\frac{8{k}^{2}-4}{1+2{k}^{2}}$,
解得xP=-$\frac{4{k}^{2}-2}{1+2{k}^{2}}$,yP=$\frac{4k}{1+2{k}^{2}}$,
令x=2,解得yM=4k,即M(2,4k),
所以$\overrightarrow{OM}$•$\overrightarrow{OP}$=2•(-$\frac{4{k}^{2}-2}{1+2{k}^{2}}$)+4k•$\frac{4k}{1+2{k}^{2}}$=4为定值.
点评 本题考查椭圆的方程的求法,注意运用待定系数法,考查直线方程和椭圆方程联立,求得交点,同时考查向量的数量积的坐标表示,属于中档题.

练习册系列答案
相关题目
18.某校为了解学生一次考试后数学、物理两个科目的成绩情况,从中随机抽取了25位考生的成绩进行统计分析.25位考生的数学成绩已经统计在茎叶图中,物理成绩如下:
90 71 64 66 72 39 49 46 55 56 85 52 6l
80 66 67 78 70 51 65 42 73 77 58 67
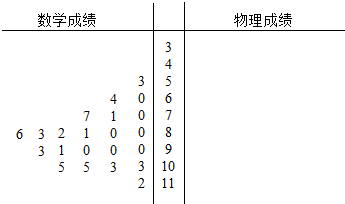
(Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计;
(Ⅱ)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图;

(Ⅲ)设上述样本中第i位考生的数学、物理成绩分别为xi,yi(i=1,2,3,…,25).通过对
样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到:
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)2=5524,$\frac{4698}{5524}$≈0.85.
求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}\overline{x}$.
90 71 64 66 72 39 49 46 55 56 85 52 6l
80 66 67 78 70 51 65 42 73 77 58 67

(Ⅰ)请根据数据在答题卡的茎叶图中完成物理成绩统计;
(Ⅱ)请根据数据在答题卡上完成数学成绩的频数分布表及数学成绩的频率分布直方图;
| 数学成绩分组 | [50,60﹚ | [60,70﹚ | [70,80﹚ | [80,90﹚ | [90,100﹚ | [100,110﹚ | [110,120] |
| 频数 |

(Ⅲ)设上述样本中第i位考生的数学、物理成绩分别为xi,yi(i=1,2,3,…,25).通过对
样本数据进行初步处理发现:数学、物理成绩具有线性相关关系,得到:
$\overline{x}$=$\frac{1}{25}$$\sum_{i=1}^{25}$xi=86,$\overline{y}$=$\frac{1}{25}$$\sum_{i=1}^{25}$yi=64,$\sum_{i=1}^{25}$(xi-$\overline{x}$)(yi-$\overline{y}$)=4698,$\sum_{i=1}^{25}$(xi-$\overline{x}$)2=5524,$\frac{4698}{5524}$≈0.85.
求y关于x的线性回归方程,并据此预测当某考生的数学成绩为100分时,该考生的物理成绩(精确到1分).
附:回归直线方程的斜率和截距的最小二乘估计公式分别为:$\widehat{b}$=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}\overline{x}$.
19.某校在一次对是否喜欢英语学科的学生的抽样调查中,随机抽取了100名同学,相关的数据如表所示:
(Ⅰ)试运用独立性检验的思想方法分析:是否有99%的把握认为“学生是否喜欢英语与性别有关?”说明理由.
(Ⅱ)用分层抽样方法在喜欢英语学科的学生中随机抽取5名,女学生应该抽取几名?
(Ⅲ)在上述抽取的5名学生中任取2名,求恰有1名学生为男性的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
| 不喜欢英语 | 喜欢英语 | 总计 | |
| 男生 | 40 | 18 | 58 |
| 女生 | 15 | 27 | 42 |
| 总计 | 55 | 45 | 100 |
(Ⅱ)用分层抽样方法在喜欢英语学科的学生中随机抽取5名,女学生应该抽取几名?
(Ⅲ)在上述抽取的5名学生中任取2名,求恰有1名学生为男性的概率.
附:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,
| p(K2≥k) | 0.100 | 0.050 | 0.025 | 0.01 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
20.为提高在校学生的安全意识,防止安全事故的发生,学校拟在未来的连续10天中随机选择3天进行紧急疏散演练,则选择的3天恰好为连续3天的概率是( )
| A. | $\frac{1}{10}$ | B. | $\frac{3}{25}$ | C. | $\frac{1}{15}$ | D. | $\frac{1}{30}$ |