题目内容
已知定点F(0,1)和直线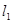 :y=-1,过定点F与直线
:y=-1,过定点F与直线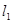 相切的动圆圆心为点C.
相切的动圆圆心为点C.
(1)求动点C的轨迹方程;
(2)过点F的直线 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线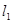 于点R,求
于点R,求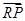 ·
· 的最小值;
的最小值;
(3)过点F且与 垂直的直线
垂直的直线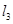 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
(1)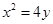 (2)16 (3)最小值32.
(2)16 (3)最小值32.
解析试题分析:(1)根据抛物线的定义可得: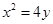 .(2)把
.(2)把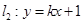 与抛物线
与抛物线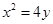 联立,再把根与系数的关系代入到
联立,再把根与系数的关系代入到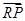 ·
· 的表达式中,最后结合基本不等式求出最小值.(3)先
的表达式中,最后结合基本不等式求出最小值.(3)先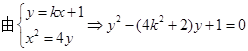 ,再
,再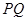 、
、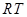 ,
,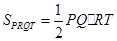 =
=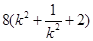 ,最后用基本不等式求出最小值.
,最后用基本不等式求出最小值.
(1)由题知点C到点F的距离等于它到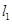 的距离,
的距离,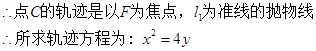
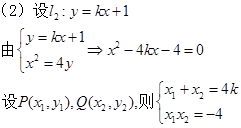
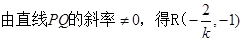
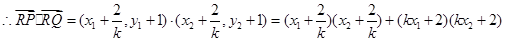
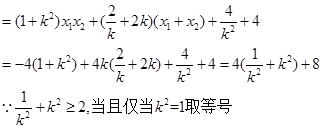
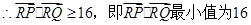
(3)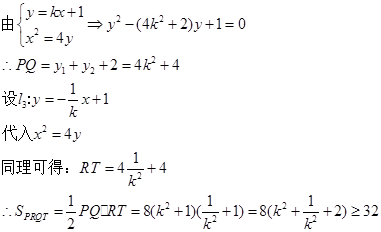
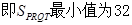
考点:抛物线的定义;根与系数的关系;基本不等式.

练习册系列答案
相关题目
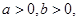 且
且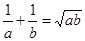
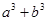 的最小值;
的最小值;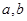 ,使得
,使得 ?并说明理由.
?并说明理由.
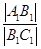 =x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;
=x(x>1),求公园ABCD所占面积S关于x的函数S(x)的解析式;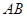 、
、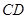 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知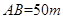 ,
,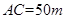 ,当
,当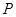 为
为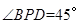 .
.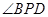 达到最大.
达到最大.
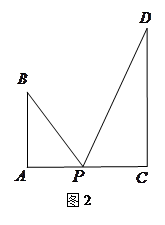
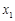 ,
, ,
,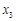 为正实数,若
为正实数,若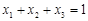 ,求证:
,求证: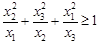 .
.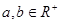 ,且
,且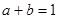 ,则
,则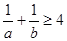 ;
;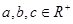 ,且
,且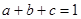 ,则
,则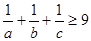 ;
;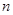 个正数
个正数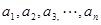 的结论?(写出结论,不必证明。
的结论?(写出结论,不必证明。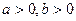 ,且
,且 ,则
,则 的最小值是
的最小值是 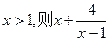 的最小值为 。
的最小值为 。