题目内容
若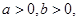 且
且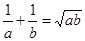
(I)求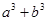 的最小值;
的最小值;
(II)是否存在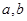 ,使得
,使得 ?并说明理由.
?并说明理由.
(1)最小值为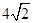 ;(2)不存在a,b,使得
;(2)不存在a,b,使得 .
.
解析试题分析:(1)根据题意由基本不等式可得: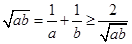 ,得
,得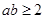 ,且当
,且当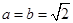 时等号成立,则可得:
时等号成立,则可得: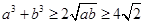 ,且当
,且当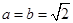 时等号成立.所以
时等号成立.所以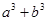 的最小值为
的最小值为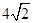 ;(2)由(1)知,
;(2)由(1)知, ,而事实上
,而事实上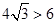 ,从而不存在a,b,使得
,从而不存在a,b,使得 .
.
试题解析:(1)由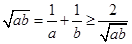 ,得
,得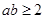 ,且当
,且当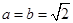 时等号成立.
时等号成立.
故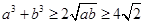 ,且当
,且当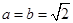 时等号成立.
时等号成立.
所以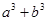 的最小值为
的最小值为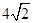 .
.
(2)由(1)知, .
.
由于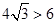 ,从而不存在a,b,使得
,从而不存在a,b,使得 .
.
考点:1.基本不等式的应用;2.代数式的处理

练习册系列答案
相关题目
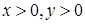 ,且
,且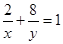 ,求
,求 及
及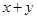 的最小值.
的最小值.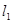 :y=-1,过定点F与直线
:y=-1,过定点F与直线 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线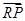 ·
· 的最小值;
的最小值;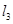 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.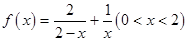 .
. 的最小值及相应
的最小值及相应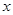 的值;
的值;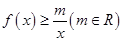 .
.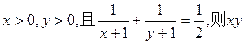 的最小值是 。
的最小值是 。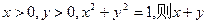 的最大值是 。
的最大值是 。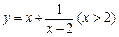 的值域是
的值域是 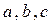 都是正数,且
都是正数,且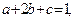 则
则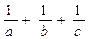 的最小值是 .
的最小值是 .