题目内容
图1是某斜拉式大桥图片,为了了解桥的一些结构情况,学校数学兴趣小组将大桥的结构进行了简化,取其部分可抽象成图2所示的模型,其中桥塔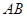 、
、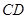 与桥面
与桥面 垂直,通过测量得知
垂直,通过测量得知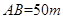 ,
,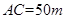 ,当
,当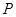 为
为 中点时,
中点时,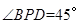 .
.
(1)求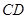 的长;
的长;
(2)试问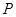 在线段
在线段 的何处时,
的何处时,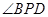 达到最大.
达到最大.
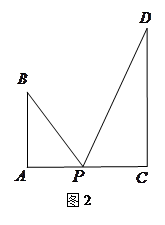
|
(1)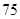 ;(2)
;(2)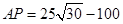 时,
时,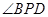 最大.
最大.
解析试题分析:(1)根据题意这实质上是一个解三角形问题,由条件可想到在两直角三角形中引入正切,即可得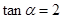 ,
,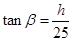 ,由两角和的正切公式可得
,由两角和的正切公式可得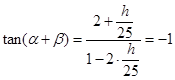 ,即可求得得
,即可求得得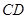 ;(2)要求
;(2)要求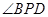 根据题意可转化为求
根据题意可转化为求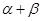 ,在两直角三角形中可得
,在两直角三角形中可得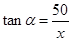 ,
,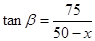 ,根据三角的关系即可得到
,根据三角的关系即可得到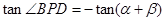 ,这样即可得到一个分式函数,利用函数的知识可想到换元,即令
,这样即可得到一个分式函数,利用函数的知识可想到换元,即令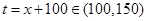 ,则
,则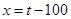 ,可得:
,可得: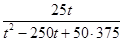 ,最后利用不等式的知识求出最值.
,最后利用不等式的知识求出最值.
(1)设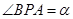 ,
,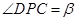 ,
,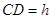 ,则
,则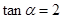 ,
,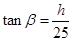 ,
,
由题意得,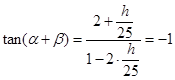 ,解得
,解得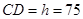 . 6分
. 6分
(2)设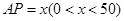 ,则
,则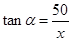 ,
,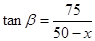 ,
,
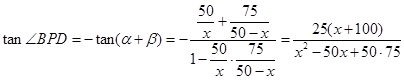 , 8分
, 8分
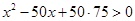 ,
,
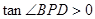 ,即
,即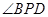 为锐角,
为锐角,
令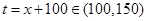 ,则
,则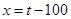 ,
,
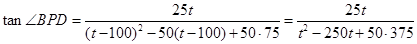 ,
,
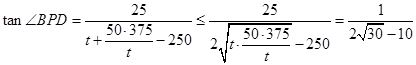 , 12分
, 12分
当且仅当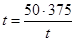 即
即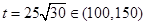 ,
,
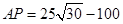 时,
时,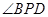 最大. 14分
最大. 14分
考点:1.解三角形;2.函数最值的求法;3.不等式的应用

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目
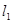 :y=-1,过定点F与直线
:y=-1,过定点F与直线 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线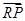 ·
· 的最小值;
的最小值;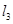 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由. ,证明
,证明
 ,
,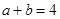 ,求证:
,求证: ;
;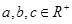 ,
,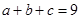 ,求证:
,求证: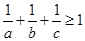 ;
; 均为正数,且
均为正数,且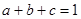
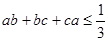 ;
;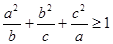 .
.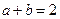 ,求证:
,求证: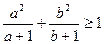
 的图象恒过定点
的图象恒过定点 ,若点
,若点 上,其中
上,其中 ,则
,则 的最小值为_______.
的最小值为_______.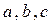 都是正数,且
都是正数,且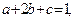 则
则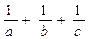 的最小值是 .
的最小值是 .