题目内容
已知x>0,y>0,且x+8y﹣xy=0.求:
(Ⅰ)xy的最小值;
(Ⅱ)x+y的最小值.
(1)32;(II)9+4 .
.
解析试题分析:(I)利用基本不等式将等式x+8y﹣xy=0构建成关于xy的不等式即可求得出xy的最小值;
(II)由x+8y=xy,变形得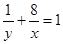 利用“乘1法”将x+y转化为:
利用“乘1法”将x+y转化为: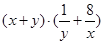 将括号打开利用基本不等式即可得出x+y的最小值.
将括号打开利用基本不等式即可得出x+y的最小值.
试题解析:(I)∵x>0,y>0,且x+8y﹣xy=0,
∴xy=x+8y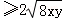 ,化为xy≥32,当且仅当x=8y=16时取等号.
,化为xy≥32,当且仅当x=8y=16时取等号.
∴xy的最小值为32;
(II)∵x>0,y>0,且x+8y﹣xy=0.
∴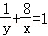 ,
,
∴x+y=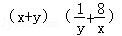 =9+
=9+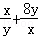 ≥
≥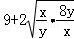 =9+4
=9+4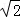 ,当且仅当x=2
,当且仅当x=2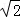 y=2
y=2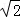 +8时取等号.
+8时取等号.
故x+y的最小值为9+4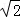
考点:基本不等式.

练习册系列答案
相关题目
 ,证明:
,证明: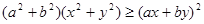 ,并利用上述结论求
,并利用上述结论求 的最小值(其中
的最小值(其中 .
.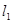 :y=-1,过定点F与直线
:y=-1,过定点F与直线 交动点C的轨迹于两点P、Q,交直线
交动点C的轨迹于两点P、Q,交直线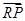 ·
· 的最小值;
的最小值;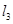 交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由.
交动点C的轨迹于两点R、T,问四边形PRQT的面积是否存在最小值?若存在,求出这个最小值;若不存在,请说明理由. ,证明
,证明
 ,
,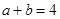 ,求证:
,求证: ;
;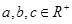 ,
,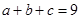 ,求证:
,求证: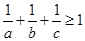 ;
; ,两侧墙的长为
,两侧墙的长为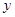 ,一套简易房所用材料费为p,试用
,一套简易房所用材料费为p,试用 。
。 ,则
,则 的最小值为
的最小值为  是互不相等的正数,则在三个不等式①
是互不相等的正数,则在三个不等式① ,②
,② ,
, 中恒成立的是_________(把你认为正确的答案的序号都填上).
中恒成立的是_________(把你认为正确的答案的序号都填上). 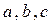 都是正数,且
都是正数,且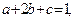 则
则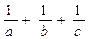 的最小值是 .
的最小值是 .