题目内容
【题目】已知数列{an}的前n项和Sn满足（p﹣1）Sn=p2﹣an（p＞0，p≠1），且a3= 
．
（1）求数列{an}的通项公式；
（2）设bn= 
，数列{bnbn+2}的前n项和为Tn ， 若对于任意的正整数n，都有Tn＜m2﹣m+ 
成立，求实数m的取值范围．
【答案】
（1）解：依题意，（p﹣1）S1=p2﹣a1（p＞0，p≠1），
∴a1=p，
∴（p﹣1）（p+a2）=p2﹣a2，解得：a2=1，
∴（p﹣1）（1+p+a3）=p2﹣a3，
又∵a3= 
，
∴（p﹣1）（1+p+ ）=p2﹣ ，解得：p=3，
∴2Sn=9﹣an，
∴2an+1=an﹣an+1，即an+1= an，
又∵a1=p=3，
∴数列{an}是首项为3，公比为 的等比数列，
∴an= 
= 
；
（2）解：由（1）可知bn= 
= 
= 
，
∴bnbn+2= 
= 
（ ﹣ 
），
∴Tn= （1﹣ + ﹣ 
+…+ ﹣ ）
= （1+ ﹣ 
﹣ ）
= 
﹣ （ + ），
显然Tn随着n的增大而增大，且Tn＜ ，
则对于任意的正整数n都有Tn＜m2﹣m+ 成立等价于对于任意的正整数n都有 ≤m2﹣m+ 成立，
化简得：m（m﹣1）≥0，
解得：m≤或m≥1．
【解析】（1）通过在（p﹣1）Sn=p2﹣an（p＞0，p≠1）中令n=1可知a1=p，令n=2可知a2=1，令n=3并结合a3= 可知p=3，进而可知数列{an}是首项为3，公比为 的等比数列，计算即得结论；（2）通过（1）可知bn= ，裂项、并项相加可知Tn= ﹣ （ + ），利用Tn＜ ，问题转化为解不等式 ≤m2﹣m+ ，计算即得结论．
【考点精析】通过灵活运用数列的前n项和和数列的通项公式，掌握数列{an}的前n项和sn与通项an的关系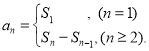
；如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式即可以解答此题．
