题目内容
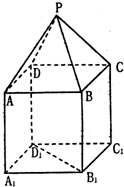 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析:由题设条件以及图形知平面PAD与平面BDD1B1的公共边为PD,平面PAD与平面BDD1B1所成的锐二面角即二面角A-PD-B,由图形的结构,两平面所成的二面角的余弦值可用三角形PAD的面积与其在面PBD上的投影面积之间的比值来表示,连接AC,BD交于一点O,可证得A0⊥面PBD,即三角形PAD在面PBD上的投影是三角形POD,求出两个三角形的面积计算其比值即可得到所求二面角的余弦值.
解答: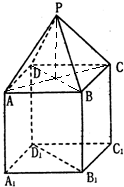 解:由题意如图,平面PAD与平面BDD1B1的公共边为PD,平面PAD与平面BDD1B1所成的锐二面角即二面角A-PD-B,连接AC,BD交于一点O,由于P-ABCD是正四棱锥,故有AO⊥面PBD,
解:由题意如图,平面PAD与平面BDD1B1的公共边为PD,平面PAD与平面BDD1B1所成的锐二面角即二面角A-PD-B,连接AC,BD交于一点O,由于P-ABCD是正四棱锥,故有AO⊥面PBD,
∴cosθ=
∵P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
.
∴BD=2
,故PO=
=
=2可求得三角形POD的面积是
×2×
=
在三角形PAD中可求得其面积是
故cosθ=
=
=
故选D
 解:由题意如图,平面PAD与平面BDD1B1的公共边为PD,平面PAD与平面BDD1B1所成的锐二面角即二面角A-PD-B,连接AC,BD交于一点O,由于P-ABCD是正四棱锥,故有AO⊥面PBD,
解:由题意如图,平面PAD与平面BDD1B1的公共边为PD,平面PAD与平面BDD1B1所成的锐二面角即二面角A-PD-B,连接AC,BD交于一点O,由于P-ABCD是正四棱锥,故有AO⊥面PBD,∴cosθ=
| S△pOD |
| S△PAD |
∵P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
| 6 |
∴BD=2
| 2 |
| PD2-OD2 |
| 6-2 |
| 1 |
| 2 |
| 2 |
| 2 |
在三角形PAD中可求得其面积是
| 5 |
故cosθ=
| S△pOD |
| S△PAD |
| ||
|
| ||
| 5 |
故选D
点评:本题考查二面角的平面角及求法,由于本题中几何图形的结构特征,采取了用投影面法求面面角的余弦,可以看到此法优点是不用作二面角的平面角,少了证明的过程,在求二面角时注意使用这一方法,其公式是锐二面角的余弦值等于投影面的面积比上原面积.本题考查了转化变形的能力以及推理运算的能力.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
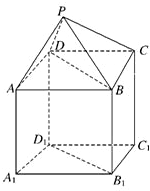 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA= 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=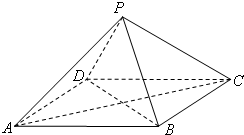 如图,P-ABCD是正四棱锥,
如图,P-ABCD是正四棱锥, 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知