题目内容
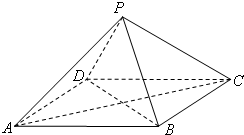 如图,P-ABCD是正四棱锥,PA=
如图,P-ABCD是正四棱锥,PA=| 3 |
(1)求证:平面PAC⊥平面PBD;
(2)求该四棱锥的体积.
分析:(1)证明AC⊥平面PBD,即可证明平面PAC⊥平面PBD;
(2)证明PO⊥平面ABCD,即可求该四棱锥的体积.
(2)证明PO⊥平面ABCD,即可求该四棱锥的体积.
解答: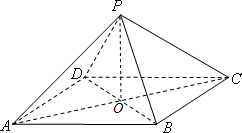 (1)证明:设AC∩BD=O,连接PO…(1分),
(1)证明:设AC∩BD=O,连接PO…(1分),
因为P-ABCD是正四棱锥,所以AC⊥BD,PO⊥AC…(3分),
因为PO∩BD=O,所以AC⊥平面PBD…(5分),
因为AC?平面PAC,所以平面PAC⊥平面PBD…(7分)
(2)解:因为AB=2,所以AO=
…(8分),
所以PO=
=1…(9分),
因为P-ABCD是正四棱锥,所以PO⊥平面ABCD…(10分)
所以,该四棱锥的体积V=
Sh=
×AB2×PO=
…(13分)(每个等号1分).
 (1)证明:设AC∩BD=O,连接PO…(1分),
(1)证明:设AC∩BD=O,连接PO…(1分),因为P-ABCD是正四棱锥,所以AC⊥BD,PO⊥AC…(3分),
因为PO∩BD=O,所以AC⊥平面PBD…(5分),
因为AC?平面PAC,所以平面PAC⊥平面PBD…(7分)
(2)解:因为AB=2,所以AO=
| 2 |
所以PO=
| PA2-AO2 |
因为P-ABCD是正四棱锥,所以PO⊥平面ABCD…(10分)
所以,该四棱锥的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查线面垂直、面面垂直,考查四棱锥体积的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
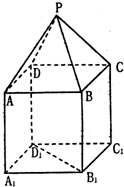 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
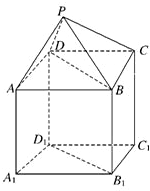 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA= 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA= 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知