题目内容
 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
| 6 |
| 5 |
| 5 |
| 6 |
| 5 |
| 5 |
分析:以A1B1为x轴,A1D1为y轴,A1A为z轴建立空间直角坐标系,求出平面PAD的法向量,
的坐标,利用距离公式,即可得到结论.
| B1A |
解答: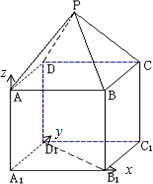 解:以A1B1为x轴,A1D1为y轴,A1A为z轴建立空间直角坐标系,
解:以A1B1为x轴,A1D1为y轴,A1A为z轴建立空间直角坐标系,
设平面PAD的法向量是
=(x,y,z),则
∵
=(0,2,0),
=(1,1,2)
∴由
,可得
取z=1得
=(-2,0,1),
∵
=(-2,0,2),
∴B1到平面PAD的距离d=
=
.
 解:以A1B1为x轴,A1D1为y轴,A1A为z轴建立空间直角坐标系,
解:以A1B1为x轴,A1D1为y轴,A1A为z轴建立空间直角坐标系,设平面PAD的法向量是
| m |
∵
| AD |
| AP |
∴由
|
|
取z=1得
| m |
∵
| B1A |
∴B1到平面PAD的距离d=
|
| ||||
|
|
| 6 |
| 5 |
| 5 |
点评:本题考查点到平面的距离,考查向量知识的运用,考查学生的计算能力,属于中档题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
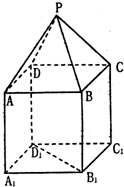 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
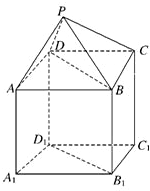 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=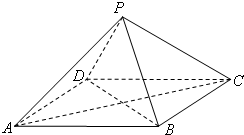 如图,P-ABCD是正四棱锥,
如图,P-ABCD是正四棱锥, 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知