题目内容
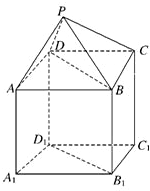 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成锐二面角的余弦值.
分析:如图,以D1为原点,D1A1所在直线为x轴,D1C1所在直线为y轴,D1D所在直线为z轴建立空间直角坐标系,给出图中各点的坐标,
(1)先计算出
,
的坐标,验证其内积为0即可得出PA⊥B1D1;
(2)平面BDD1B1的法向量为
=(-2,2,0).故再求出平面PAD的法向量
,设所求锐二面角为θ,由公式cosθ=
(1)先计算出
| AP |
| D1B1 |
(2)平面BDD1B1的法向量为
| AC |
| n |
|n•
| ||
|n|•|
|
解答: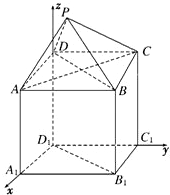 解:以D1为原点,D1A1所在直线为x轴,D1C1所在直线为y轴,D1D所在直线为z轴建立空间直角坐标系,
解:以D1为原点,D1A1所在直线为x轴,D1C1所在直线为y轴,D1D所在直线为z轴建立空间直角坐标系,
则D1(0,0,0),A1(2,0,0),B1(2,2,0),C1(0,2,0),
D(0,0,2),A(2,0,2),B(2,2,2),C(0,2,2),
P(1,1,4).
(1)证明:∵
=(-1,1,2),
=(2,2,0),
∴
•
=-2+2+0=0,
∴PA⊥B1D1.
(2)平面BDD1B1的法向量为
=(-2,2,0).
=(2,0,0),
=(1,1,2).
设平面PAD的法向量为
=(x,y,z),则
⊥
,
⊥
.
∴
∴
.取
=(0,-2,1),
设所求锐二面角为θ,则
cosθ=
=
=
.
 解:以D1为原点,D1A1所在直线为x轴,D1C1所在直线为y轴,D1D所在直线为z轴建立空间直角坐标系,
解:以D1为原点,D1A1所在直线为x轴,D1C1所在直线为y轴,D1D所在直线为z轴建立空间直角坐标系,则D1(0,0,0),A1(2,0,0),B1(2,2,0),C1(0,2,0),
D(0,0,2),A(2,0,2),B(2,2,2),C(0,2,2),
P(1,1,4).
(1)证明:∵
| AP |
| D1B1 |
∴
| AP |
| D1B1 |
∴PA⊥B1D1.
(2)平面BDD1B1的法向量为
| AC |
| DA |
| OP |
设平面PAD的法向量为
| n |
| n |
| DA |
| n |
| DP |
∴
|
|
| n |
设所求锐二面角为θ,则
cosθ=
|n•
| ||
|n|•|
|
| |0-4+0| | ||||
2
|
| ||
| 5 |
点评:本题考查用空间向量求直线与平面的夹角以及用空间向量证明面面垂直,正确解题的前提是理解向量内积与两直线位置的对应关系及两平面法向量的夹角的余弦的绝对值即两平面夹角的余弦值,了解知识之间的衔接点,是正确转化的关键.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
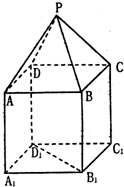 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=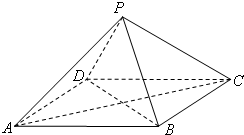 如图,P-ABCD是正四棱锥,
如图,P-ABCD是正四棱锥, 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知