Question

已知平面区域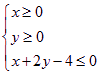恰好被面积最小的圆  

及其内部所覆盖．

(1)试求圆的方程.

(2)若斜率为1的直线与圆C交于不同两点满足,求直线的方程.

Answer 1

(1)

(2)

解析:

(1)由题意知此平面区域表示的是以构成的三角形及其内部,且△是直角三角形,

所以覆盖它的且面积最小的圆是其外接圆,故圆心是(2,1),半径是,

所以圆的方程是…………………6分

   (2)设直线的方程是:. 

     因为,所以圆心到直线的距离是, ………………………8分

即    解得:.   ………………………………10分

所以直线的方程是:…………12分