Question

(本题满分12分) 已知平面区域恰好被面积最小的圆C：及其内部覆盖．

（1）求圆C的方程；

（2）斜率为1的直线与圆C交于不同两点A、B，且，求直线的方程．

 

Answer 1

【答案】

(1) =5；（2） 。

【解析】本试题主要是考查了圆的方程，以及直线与圆的位置关系的运用。

（1）由题意知此平面区域表示的是以构成的三角形及其内部

且⊿是直角三角形，所以覆盖它的且面积最小的圆是其外接圆，从而得到圆心和半径。

（2）设直线的方程是： 

因为⊥,所以圆C到直线的距离是

进而求解得到直线方程。

                                                                                                                                                                                                                                                                               解：(1)由题意知此平面区域表示的是以构成的三角形及其内部

且⊿是直角三角形，所以覆盖它的且面积最小的圆是其外接圆-------------2分

故圆心是（2,1），半径是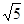，所以圆C的方程是=5----------6分

（2）设直线的方程是：                -----------------7分

因为⊥,所以圆C到直线的距离是   

                              --------------10分

解得            

所以直线的方程是：           ---------------12分