题目内容
7．等比数列{an}的前n项和为Sn=a•2n+a-2，则an=2n-1．分析 由题意可表示数列的前3项，由等比数列可得a值，可得数列的首项和公比，可得通项公式．
解答 解：由题意可得a1=S1=a•21+a-2=3a-2，
a2=S2-S1=a•22-a•21=2a，
a3=S3-S2=a•23-a•22=4a，
由等比数列可得（2a）2=4a（3a-2），
解得a=0或a=1，
当a=0时a2=2a=0，不能为等比数列的项，应舍去，
∴a=1，∴a1=3a-2=1，a2=2a=2，公比q=2
∴an=1×2n-1=2n-1，
故答案为：2n-1
点评 本题考查等比数列的求和公式和通项公式，求出a的值是解决问题的关键，属基础题．
练习册系列答案
相关题目
17．
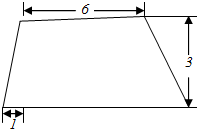已知一圆台的轴截面如图所示，则它的内接四棱台体积的最大值为（ ）
已知一圆台的轴截面如图所示，则它的内接四棱台体积的最大值为（ ）| A． | 37 | B． | 74 | C． | 111 | D． | 222 |
18．一个几何体的三视图如图所示，则该几何体的体积为（ ）
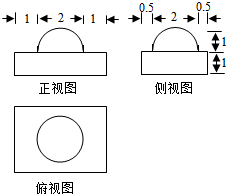
| A． | 12+$\frac{π}{3}$ | B． | 12+$\frac{2π}{3}$ | C． | 12+π | D． | 12+$\frac{4π}{3}$ |
15．已知x、y∈（-$\sqrt{2}$，$\sqrt{2}$），且x•y=1，则$\frac{2}{2-{x}^{2}}$+$\frac{4}{4-{y}^{2}}$的最小值为（ ）
| A． | $\frac{20}{7}$ | B． | $\frac{12}{7}$ | C． | $\frac{16+4\sqrt{2}}{7}$ | D． | $\frac{16-4\sqrt{2}}{7}$ |
12．已知等差数列{an}满足a2=3，a5=9，若数列{bn}满足b1=3，bn+1=abn，则{bn}的通项公式为bn=（ ）
| A． | 2n-1 | B． | 2n+1 | C． | 2n+1-1 | D． | 2n-1+2 |
19．定义在N*上的函数f（x）满足f（1）=1，且f（n+1）=$\left\{\begin{array}{l}{\frac{1}{2}f（n），n为偶数}\\{f（n），n为奇数}\end{array}\right.$，则f（22）=（ ）
| A． | $\frac{1}{1024}$ | B． | $\frac{1}{512}$ | C． | $\frac{1}{2048}$ | D． | 1 |
如图，有一块边长为15cm的正方形铁皮，将其四个角各截去一个边长为x cm的小正方形，然后折成一个无盖的盒子．